This post is the third one of a series regarding loops in R an Python.
The first one was Different kinds of loops in R. The recommendation is to use different kinds of loops depending on complexity and size of iterations.
The second post was Loop-Runtime Comparison R, RCPP, Python to show performance of parallel and sequencial processing for non-costly tasks.
This post is about costly tasks.
Frequently, for non-costly tasks multiprocessing is not appropriate. Until a certain degree of complexity, the distribution of tasks to the cores (processor management) is more costly than running the loop in a sequence. Specifically, in case of Python this is an issue due to the Global Interpreter Lock (GIL).
The challenge is to investigate which one (R or Python) is more favourable for dealing with large sets of costly tasks. For comparison purpose both a sequential for loop and multiprocessing is used – in Python and R as well.
In this particular case, the task is to check whether a certain number is a prime number or not. For simplification, the test starts from 3 instead of 2.
Machine is:
i7 8700k, 16Gb GDDR5 RAM.
The R code:
###################################################################################################
library(parallel)
NumOfCores <- detectCores() – 1
clusters <- makeCluster(NumOfCores)
size <- c(100, 1000, 10000, 20000, 30000, 40000, 50000)
rep <- rep(0, times = length(size))
z = 1
Prim <- function(i) {
chech_vec = (i – 1):2
P = i %% chech_vec
if (any(P == 0)) {
return(“n”)
} else {
return(“y”)
}
}
for(j in size){
start = Sys.time()
PrimNum <- parSapply(cl = clusters, X = 3:j, FUN = Prim)
end = Sys.time()
rep[z] = end – start
z = z + 1
}
z=1
for(j in size){
PrimNum = rep(NA, times = (j))
start = Sys.time()
for(i in 3:j){
PrimNum[i-2] <- Prim(i)
}
end = Sys.time()
rep[z] = end – start
z = z + 1
}
###################################################################################################
The equivalent Python code:
###################################################################################################
import time
import numpy as np
import multiprocessing
from joblib import delayed, Parallel, parallel_backend
cores = multiprocessing.cpu_count() – 1
size = [101, 1001, 10001, 20001, 30001, 40001, 50001]
rep = [0]*len(size)
z = 0
def Prim(i):
chech_vec = list(range(2,(i)))
P = np.mod(i , chech_vec)
if any(P == 0):
return “n”
else:
return “y”
#Changing the inner_max_num_threads does not matter. Furthermore, for this task a backend =”threading” is even slower.
for j in size:
start = time.time()
if __name__ == “__main__”:
with parallel_backend(“loky”, inner_max_num_threads=2):
PrimNum = Parallel(n_jobs = cores)(delayed(Prim)(i) for i in range(3,j))
end = time.time()
rep[z] = end – start
z += 1
z = 0
for j in size:
PrimNum = [0]*j
start = time.time()
for i in range(3,j):
PrimNum[i] = Prim(i)
end = time.time()
rep[z] = end – start
z += 1
###################################################################################################
Results are:
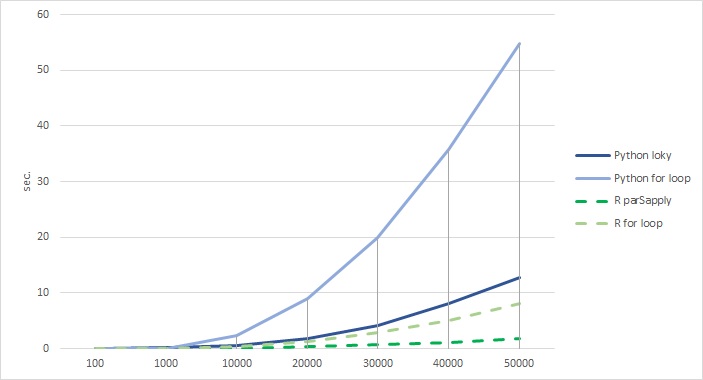
The clear winner is R with significantly faster loops for computing prime numbers in this constellation.
