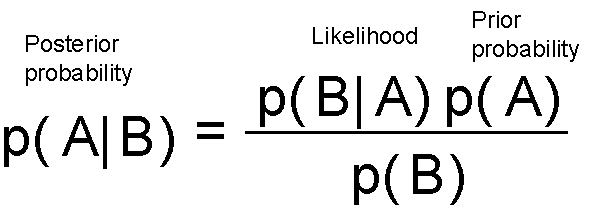This article was written by Tirthajyoti Sarkar.
Acknowledgements
Thanks to my CS7641 class at Georgia Tech in my MS Analytics program, where I discovered this concept and was inspired to write about it. Thanks to Matthew Mayo for editing and re-publishing this in KDnuggets.
Introduction
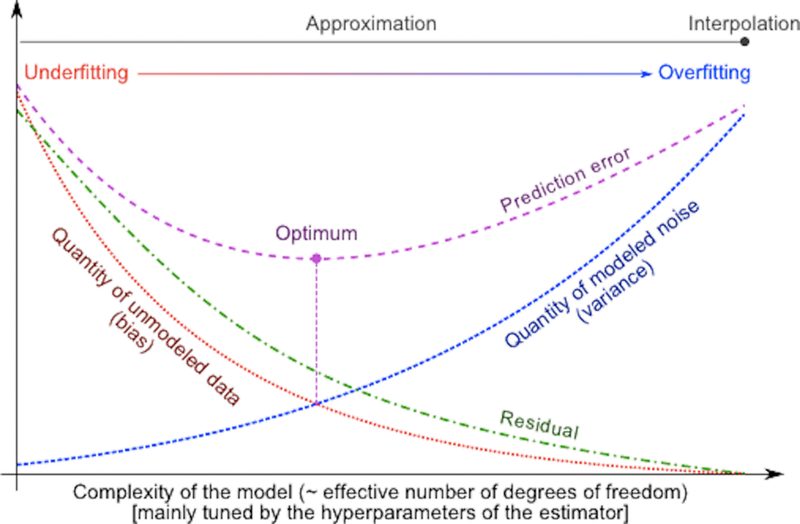
It is somewhat surprising that among all the high-flying buzzwords of machine learning, we don’t hear much about the one phrase which fuses some of the core concepts of statistical learning, information theory, and natural philosophy into a single three-word-combo.
Moreover, it is not just an obscure and pedantic phrase meant for machine learning (ML) Ph.Ds and theoreticians. It has a precise and easily accessible meaning for anyone interested to explore, and a practical pay-off for the practitioners of ML and data science.
I am talking about Minimum Description Length. And you may be thinking what the heck that is…
Let’s peel the layers off and see how useful it is…
Bayes and his Theorem
We start with (not chronologically) with Reverend Thomas Bayes, who by the way, never published his idea about how to do statistical inference, but was later immortalized by the eponymous theorem.
It was the second half of the 18th century, and there was no branch of mathematical sciences called “Probability Theory”. It was known simply by the rather odd-sounding “Doctrine of Chances” — named after a book by Abraham de Moievre. An article called, “An Essay towards solving a Problem in the Doctrine of Chances”, first formulated by Bayes, but edited and amended by his friend Richard Price, was read to Royal Society and published in the Philosophical Transactions of the Royal Society of London, in 1763. In this essay, Bayes described — in a rather frequentist manner — the simple theorem concerning joint probability which gives rise to the calculation of inverse probability i.e. Bayes Theorem.
Many a battle have been fought since then between the two warring factions of statistical science — Bayesians and Frequntists. But for the purpose of the present article, let us ignore the history for a moment and focus on the simple explanation of the mechanics of the Bayesian inference.
In the world of statistical inference, a hypothesis is a belief. It is a belief about about the true nature of the process (which we can never observe), that is behind the generation of a random variable (which we can observe or measure, albeit not without noise). In statistics, it is generally defined as a probability distribution. But in the context of machine learning, it can be thought of any set of rules (or logic or process), which we believe, can give rise to the examples or training data, we are given to learn the hidden nature of this mysterious process.
To read the whole article, click here.