
“Fail fast, pivot, and try again” is the heart of learning. And in knowledge-based industries, the economies of learning are more powerful than the economies of scale.
In February 2020, Dr. Anthony Fauci wrote that store-bought face masks would not be very effective at protecting against the COVID-19 pandemic and advised a traveler not to wear one. Based on the available data at the time, it seemed like the right decision. However, over the next several months, data-based evidence built up supporting masks in preventing the spread of the COVID droplets from sneezing, coughing, and even talking that can lead to the spread of the COVID virus.
This is an important example of how we humans learn. We make an assumption based upon the data that we currently have (that we didn’t need to wear a mask) and then we update those assumptions as we gather more evidence and data (yes, we probably should be wearing masks). We make assumptions based upon the data available to us, and then we learn as we gather more data.
This establishing of a prior probability, gathering more data (evidence), and then updating those prior assumptions (posterior probability) is the heart of how Artificial Intelligence and Machine models learn. And the learning process that is the basis for much of the AI / ML that occurs today is based upon the concept called Bayesian Inference.
Bayesian inference is a method of statistical inference in which Bayes’ theorem is used to update the probability for a hypothesis as more evidence or information becomes available.
Bayesian inference is a method of statistical inference in which Bayes’ theorem is used to update the probability for a hypothesis as more data or evidence is gathered.
Now, I’m certainly not a statistician (I’ve been reminded of that on social media more than once) but let me share how I explain how Bayesian Inference underpins the way that AI / ML models – and humans – learn.
How Bayesian Inference Works
Like in the Dr. Fauci example, we leverage currently available (historical) data to create an assumption or a prior probability distribution.
Prior Probability Distribution (Prior) is the probability of the occurrence of an event based on established or historical patterns, trends, and relationships found in the historical data.
Yes, based upon the best data available to use, we make assumptions (Figure 1).
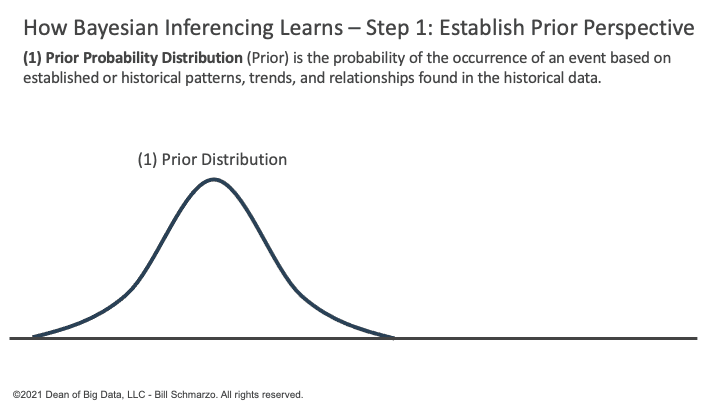
Figure 1: Bayesian Inferencing: Step 1: Establish Prior Perspective
But as we learned during the pandemic, new data or evidence emerges that challenges our original assumptions.
Evidence Probability Distribution (Evidence) is the probability of the occurrence of an event based upon current data (Figure 2).
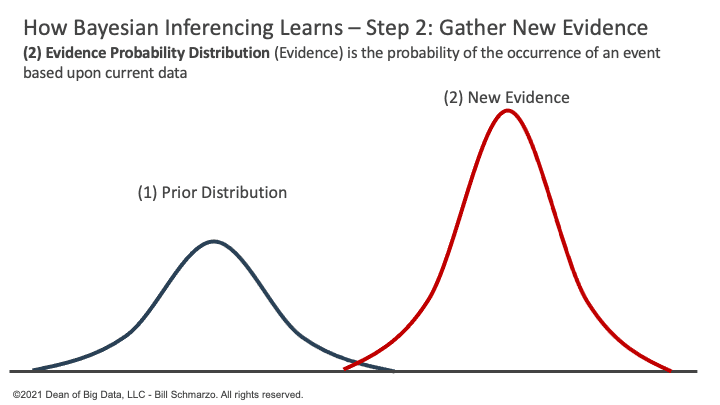
Figure 2: Bayesian Inferencing: Step 2: Gather New Evidence
We should always seek to gather more data or evidence to become more informed in our decision-making.
So, what do we do with this new evidence? We adjust our prior probability distribution to reflect the new evidence and create a posterior probability distribution.
Posterior Probability Distribution (Posterior) represents the probability of the occurrence of an event based upon updating the Prior Distribution with the more current Evidence Distribution.
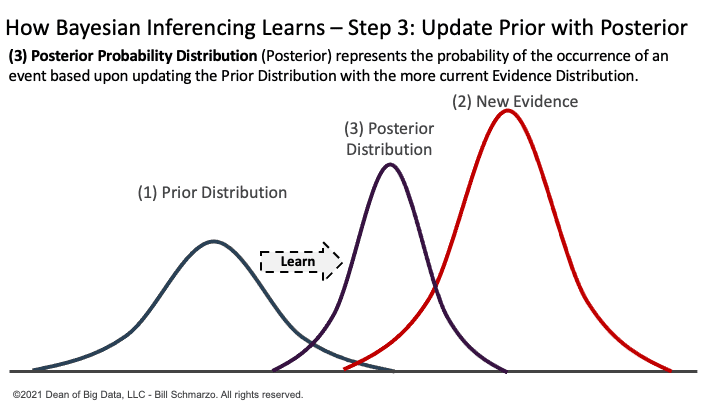
Figure 3: Bayesian Inferencing: Step 3: Update Posterior Probability Distribution
This Bayesian Inferencing concept is the underlying principle for how AI models continuously learn and adapt.
How Does Artificial Intelligence (AI) Work
Conceptually, an AI model is quite simple. An AI model continuously interacts or engages with its environment seeking to optimize its desired or optimal outcomes measured against the metrics and variables that comprise the AI Utility Function (Figure 4).
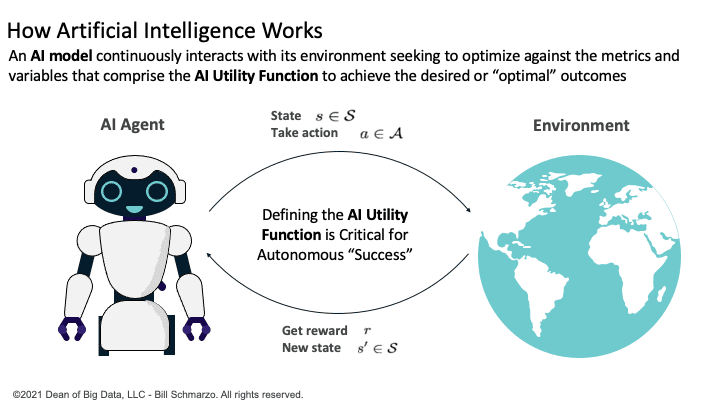
Figure 4: How AI Models Learn
AI models learn through the following process:
- The AI Engineer (in very close collaboration with the business stakeholders) defines the AI Utility Function, which are the metrics and variables against which the AI model’s progress and success will be measured.
- The AI model operates and interacts within its environment using the AI Utility Function to gain feedback in order to continuously learn and adapt its performance (using backpropagation and stochastic gradient descent to constantly tweak the models weights and biases).
- The AI model seeks to make the “right” or optimal decisions, as framed by the AI Utility Function, as the AI model interacts with its environment.
Bottom-line: the AI model seeks to maximize “rewards” based upon optimizing the “values” as articulated by the metrics and variables that comprise the AI Utility Function.
Summary: Bayesian Inference and Economies of Learning
Economies of Learning measures an organization’s economic value creation effectiveness as it seeks to continuously learn and adapt to changes in its business and operating environment.
In knowledge-based industries, the Economies of Learning can be augmented by integrating AI / ML to create assets, processes, and policies that continuously learn and adapt to their operating environment…with minimal human intervention (Figure 5).
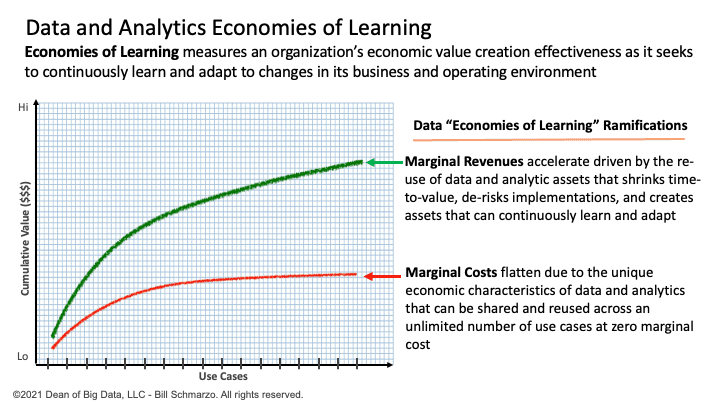
Figure 5: The Benefits of the Economies of Learning
In a world of AI / ML-driven value creation, Bayesian Inferencing is the heart of exploiting the economies of learning.
“Fail fast, pivot, and try again” is the heart of learning. And in knowledge-based industries, the economies of learning are more powerful than the economies of scale.
