Tools such as OpenAI can on occasion give the impression that they are able to prove theorems and even generalize them. Whether this is a sign of real (artificial) intelligence or simply combining facts retrieved from technical papers and put things together without advanced logic, is irrelevant. A correct proof is a correct proof, no matter how the author – a human or a bot – came to it.
My experience is that tools like OpenAI make subtle mistakes, sometimes hard to detect. Some call it hallucinations. But the real explanation is that usually, it blends different results together and add transition words between sentences in the answer, to make it appear as a continuous text. Sometimes, this creates artificial connections between items that are loosely if at all related, without providing precise reference to the source, and the exact location within each reference. It makes it hard to double check and make the necessary corrections. However, the new generation of LLMs (see here) offers that capability: deep, precise references.
Likewise, mathematicians usually make mistakes in the first proof of a new, challenging problem. Sometimes these are glitches that you can fix, sometimes the proof is fundamentally wrong and not fixable. It usually takes a few iterations to get everything right.
Make AI your Collaborator, not your Enemy
Many see AI as the enemy lurking around to take your job. At the other end of the spectrum, many see AI as the panacea to fully automate intellectual work and replace all humans down the line, including lawyers, doctors, engineers, artists, and mathematicians. As always, the best is in the middle: get AI to help the human, and have AI take input from humans to help itself. This is called collaboration. These days, with LLM 1.0, the latter is done via prompt engineering. In LLM 2.0, a much better UI allows the human to interact more efficiently with AI, see here.
A mathematical proof that answers a difficult question can be as long as a 100-page book, and involves many components, with steps and sub-steps in each component. AI can help in various ways:
- Solve some steps or sub-steps. In some cases, get hard-to-find references offering a solution or related results to some step, so that you are not reinventing the wheel.
- Automate mechanical mathematical computations without generating error (symbolic math) saving many hours of boring work.
- Verify some intermediate results or identify the exact value or range of some intermediate constants involved in the proof.
- Double check the validity of your statements, detect errors in your argumentation. Simplify your argumentation.
- Generate efficient code for validation purposes, for instance dealing with very big numbers and computer-intensive simulations.
Case Study: Are the Digits of 𝞹 Random?
This maybe the easiest conjecture to state. Kids in elementary school understand the question. Yet it is possibly the deepest and most fascinating one. By random, I mean undistinguishable from a string of random bits. Empirical evidence shows that it could be true, based on the first 20 trillion digits or so: they pass all tests of randomness. Yet no one knowns if at some point, perhaps after 50 quadrillion digits, only 3s and 5s are left. The only thing known for sure is that the digit sequence is non periodic.
What if you could use AI to make progress towards a deep result? The first step is to formulate very basic questions and try to find some new framework that may lead to an answer, any answer. This is what I did. I ended up with the number e instead (Euler’s number — the lowest hanging fruit), its binary digits, and answering whether or not the proportion of 1 is strictly positive. This is not a trivial question despite appearances. No one has ever answered it with a formal proof. Indeed, proving it would be the first deep mathematical result ever obtained for any major math constant. By contrast, you can prove that there are at least √n digits equal to 1 in the first n digits of √2. But this is by no means a deep result, and relatively easy to prove. And this is the best that we knew so far, until I published my result about e earlier this week!
How AI Helped me Obtain Ground-breaking Results
The results in question, regarding the digit distribution of e, are published as paper 51, here. Now I explain how AI helped me with critical steps towards building the architecture of the new theory to obtain the seminal results.
Step 1
It first starts with computing the binary digits of 210000 + 1 at power 210000. Note that this number is so big that no computer system in the universe will ever be able to handle it, even if given trillions of years. It dwarfs the 20 trillion digits computed so far by the most powerful computers. Of course, I used some tricks. Also, it guarantees that no one else ever explored that path, making it the first experiment of this scale in mathematical history. As a side note, the first 10,000 binary digits of that number match those of e, but there is a lot more to it if you look at my paper. Here AI helped me get efficient code and double-check the precision.
Step 2
The second step consists of looking at the patterns that emerge when dealing with such numbers, not visible with smaller numbers. The technical details are unimportant to the layman — they are in the paper. What matters here are specific aspects of the methodology and where I got help from my friend AI. The featured picture revealed interesting patterns described in the paper, leading to a deeper dive, resulting in the picture below.
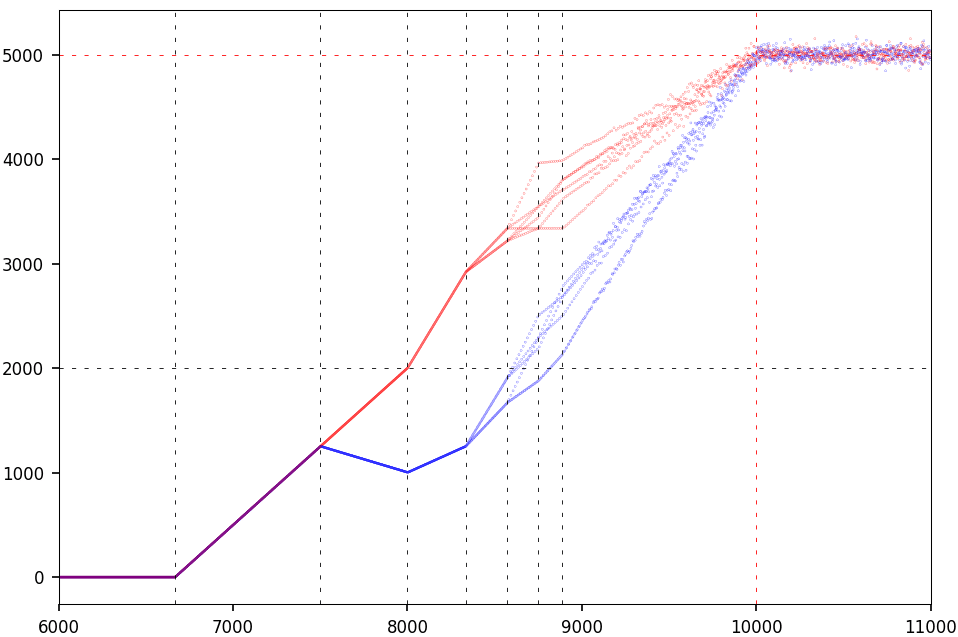
Figure 1 shows the typical behavior of a dynamical system in non-chaotic regime, before entering chaos at 10,000 on the horizontal axis. Digits are computed via self-convolution of strings, and at 10,000 they match the first 10,000 binary digits of e. Here is how AI helped:
- Detecting the widths of the successive bands delimited by the vertical dashed lines. These widths are exactly proportional to 1/2, 1/6, 1/12, 1/20, 1/30 and so on. It found the exact pattern.
- The number of segments in each vertical band is not arbitrary, but proportional to a sequence of factorial numbers. AI was able to get the exact pattern.
- When averaging the segments, you get a perfect straight line, pictured in the detailed paper. The chaotic zone at the top right corner shows a Gaussian behavior and flattens to a horizontal line when increasing from 10,000 to infinity. AI helped with this.
While I used AI mostly for empirical confirmation and pattern detection, in the end it helped build a robust proof. AI spared me many hours of work, also helping me find relevant references. The rest is history.
About the Author
Vincent Granville is a pioneering GenAI scientist and machine learning expert, co-founder of Data Science Central (acquired by a publicly traded company in 2020), Chief AI Scientist at MLTechniques.com and GenAItechLab.com, former VC-funded executive, author (Elsevier) and patent owner — one related to LLM. Vincent’s past corporate experience includes Visa, Wells Fargo, eBay, NBC, Microsoft, and CNET. Follow Vincent on LinkedIn.
