In my ground-breaking paper 51 available here, I paved the way to solve a famous multi-century old math conjecture. The question is whether or not the digits of numbers such as π are evenly distributed. Currently, no one knows if the proportion of ‘1’ even exists in these binary digit expansions. It could oscillate forever without ever converging. Of course, mathematicians believe that it is 50% in all cases. Trillions of digits have been computed for various constants, and they pass all randomness tests. In this article, I offer a new framework to solve this mystery once for all, for the number e.
Rather than a closure on this topic, it is a starting point opening new research directions in several fields. Applications include cryptography, dynamical systems, quantum dynamics, high performance computing, LLMs to answer difficult math questions, and more. The highly innovative approach involves iterated self-convolutions of strings and working with numbers such as 2n + 1 at power 2n, with n larger than 100,000. No one before has ever analyzed the digits of such titanic numbers!
I first provide an overview of the discovery in layman’s terms, then discuss the implications, and finally offer a challenge to work on a final proof. Use any AI tool you want to work for the challenge. The goal is to see how AI and LLMs can handle this problem and outperform humans!
1. The Mathematical Breakthrough, in Layman’s Terms
In the original version of the paper, I use strings, making the link to LLMs more obvious. However, it is easier to explain the theory using numbers rather than strings. By definition, S(n, k) represents the number 2n + 1 at power 2k. The first result (easy to prove) is that the first n-3 binary digits of S(n, n) match those of the number e. The difficult step is to prove that the proportion of ‘1’ in S(n, n) approaches 50% as n tends to infinity. For any fixed n, the results remain true if we compute S(n, k) iteratively with the formula S(n, k+1) = S2(n, k) and we only keep the first 2n bits on the left at each iteration. This fact is also easy to prove.
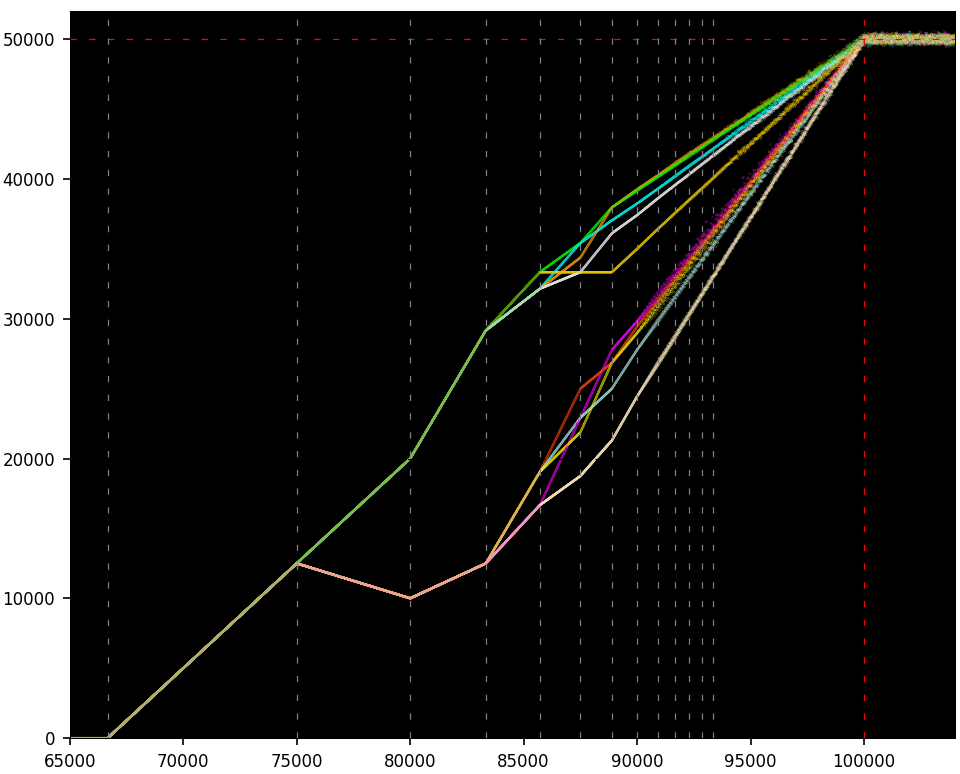
For each n, the sequence {S(n, k)} indexed by k is a dynamical system: the same one for each n but with a different seed S(n, 0) that depends on n. If k is no larger than n, we stay in the non-chaotic regime at all times. This is always the case here. Details are beyond the scope of this article. However, Figure 1 summarizes what is happening.
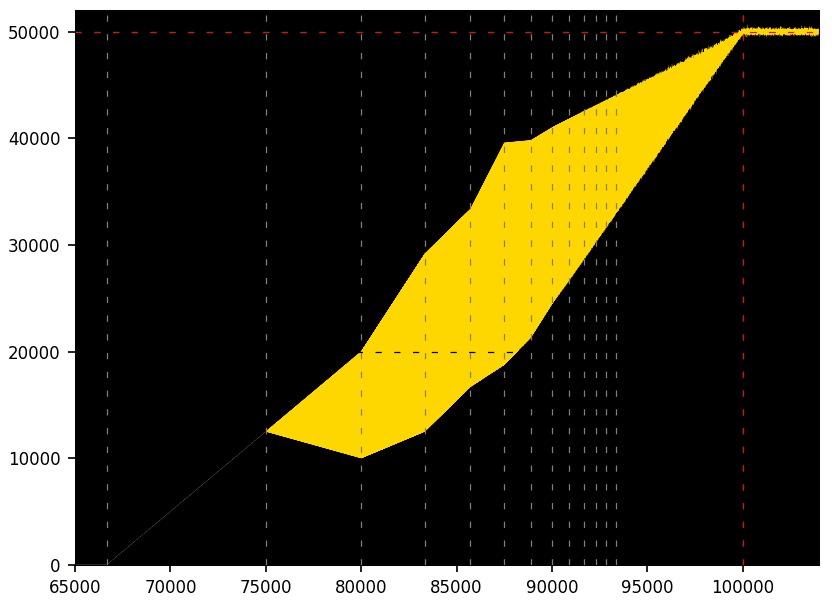
Figure 2 is the default picture that you obtain with a standard plot, connecting the successive dots in Figure 1 with a line segment. It produces a time series, more specifically a quantum time series here. You need a scatterplot to see the spectacular patterns hidden beneath the surface. Nevertheless, Figure 2 shows the potential range for the number of ‘1’ in S(k, n), given k on the X-axis and n = 100,000. It shows that the proportion of ‘1’ must lie within the yellow area at all times. Determining the piecewise linear boundary of the yellow area is enough to prove the conjecture. The horizontal stochastic yellow band on the right, when k > n, reduces to a line segment when n is infinite, confirming that the proportion of ‘1’ tends to 50%.
2. Cool Applications
The first obvious application is cryptography, more specifically pseudo-random generators. Instead of using the seed S(n, 0) = 2n + 1, start with an arbitrary seed. Then the fully chaotic phase starts almost immediately rather than when k = n. The connection to quantum dynamics and quantum entropy is evident in Figure 1. Also, the framework features interesting dynamical systems with potential applications to modeling in various fields. In particular, in the context of computer-intensive simulations or agent-based modeling. In particular, see an application of the digit count function in the recent article “Maximum Mutational Robustness in Genotype–Phenotype Maps Follows a Self-similar Blancmange-like Curve” (The Royal Society Publishing, 2023).
The link between iterated self-convolutions (the core of our method) and convergence to a Gaussian distribution when k > n and chaos starts, is of special interest. Also, dealing with gigantic numbers requires HPC (High Performance Computing) and special methods in numerical analysis. This opens up new research areas. Finally, for the connection to LLMs, in particular testing their ability to solve difficult math problems, see next sections.
Rather than a final closure on the infamous conjecture, my framework offers a starting point to jump-start research in various domains. I hope that it will lead to fertile and original scientific activity, with many scientists as well as AI further contributing to the next round of discoveries, in years to come.
3. Dataset to Benchmark Mathematical Abilities of LLMs
Blending AI with human intelligence is the way to go to solve the hardest problems. I did my part to help AI. Now I invite you to use AI to help finalize. The goal is to solve this famous multi-century old problem. Along the way, establishing the strongest possible conclusions, as well as rating various LLMs on their math capabilities, on a problem far beyond PhD level, yet explainable in layman’s terms. The following list features the top questions to address:
- In figure 1 with n = 100,000, given S(n, k), S(n, k-1), S(n, k-2) and so on, can you predict S(n, k+1), S(n, k+2) and so on? This is a typical LLM problem: predicting future sentences given past sentences, with S(n, k) being the current sentence. Here the alphabet consists of ‘0’ and ‘1’, and we only care about the number of ‘1’ in the first n characters of each sentence, for values of k such as the ratio k / n is between 80% and 100%.
- The first bifurcation in Figure 1 occurs at k = 75,000. From there the green segment going up corresponds to even values of k, and the orange segment going down to odd values. The second bifurcation occurs at k = 80,000, with no split this time, just a change in slopes. Identify all bifurcation points, the number of segments in each band delimited by successive vertical dashed lines, the slope of each segment, and which values of k are attached to each segment. In Figure 1, the color corresponds to the value of k modulo 12.
- Try with n as large as possible, focusing on values of k such that the ratio k / n is above 80%. Note that the vertical dashed lines show when bifurcations occur.
- Do the same with the seeds 2n + 3 and 2n – 1, leading respectively to the binary digits of the cube and inverse of Euler’s number e.
The more precise answers you get to these questions, the more easily a human being can take over the results obtained with AI, to complete the proof: the fact that when k = n, the proportion of ‘1’ is close enough to 50%, and tends to 50% as n tends to infinity.
To produce the LLM benchmark dataset with the strings S(n, k), use the source code posted here on GitHub. For more information, see paper 51 posted here.
About the Author

Vincent Granville is a pioneering GenAI scientist, co-founder at BondingAI.io, the LLM 2.0 platform for hallucination-free, secure, in-house, lightning-fast Enterprise AI at scale with zero weight and no GPU. He is also author (Elsevier, Wiley), publisher, and successful entrepreneur with multi-million-dollar exit. Vincent’s past corporate experience includes Visa, Wells Fargo, eBay, NBC, Microsoft, and CNET. He completed a post-doc in computational statistics at University of Cambridge.
