This problem appeared as an assignment in the coursera course Natural Language Processing (by Stanford) in 2012. The following description of the problem is taken directly from the assignment description.
In this article, a probabilistic parser will be built by implementing the CKY parser. The Manually Annotated Sub-Corpus (MASC) from the American National Corpus (ANC): This will be used for this purpose.
Instructions
First, we need to learn a PCFG from the training trees. Since the training set is handparsed this learning is very easy. We need to simply set:
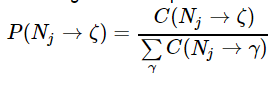
where C(N_j→ζ) is the count observed for that production in the data set. While we could consider smoothing rule rewrite probabilities, it is sufficient to just work with un-smoothed MLE probabilities for rules. (Doing anything else makes things rather more complex and slow, since every rewrite will have a nonzero probability, so let’s get things working with an un-smoothed grammar before considering adding smoothing!).
At the very beginning, all the train and the test trees are read in. The training trees are going to be used to construct a PCFG parser, by learning the PCFG grammar. The parser is then used to predict trees for the sentences in the test set. For each test sentence, the parse given by the parser is evaluated by comparing the constituents it generates with the constituents in the hand-parsed version. From this, precision, recall and the F1 score are calculated.
There are the following basic data structures:
• ling.Tree: CFG tree structures (ling.Trees.PennTreeRenderer)
• Lexicon: Pre-terminal productions and probabilities
• Grammar, UnaryRule, BinaryRule: CFG rules and accessors
Most parsers require grammars in which the rules are at most binary branching. Hence, first we need to binarize the trees and then construct a Grammar out of them using MLE.
The Task
The first job is to build a CKY parser using this PCFG grammar learnt. Scan through a few of the training trees in the MASC dataset to get a sense of the range of inputs. Something worth noticing is that the grammar has relatively few non-terminal symbols but thousands of rules, many ternary-branching or longer. Currently there are 38 MASC train files and 11 test files.
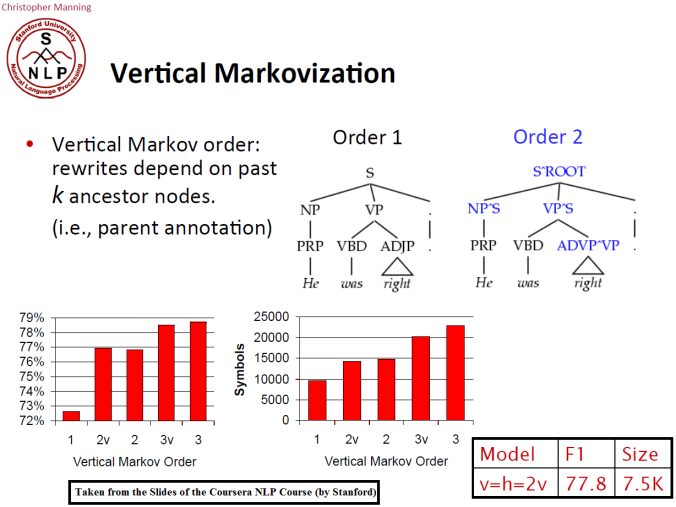
Once we have a parser working on the treebank, the next task is improve upon the supplied grammar by adding 1st / 2nd-order vertical markovization. This means using parent annotation symbols like NP^S to indicate a subject noun phrase instead of just NP.
The Dynamic Programming Algorithm (CKY) for Parsing
The following figure shows the CKY algorithm to compute the best possible (most probable) parse tree for a sentence using the PCFG grammar learnt from the training dataset.

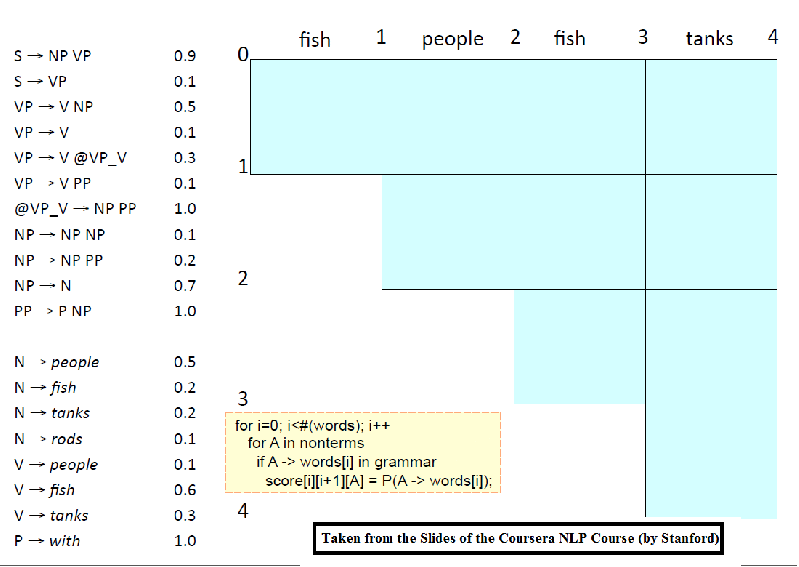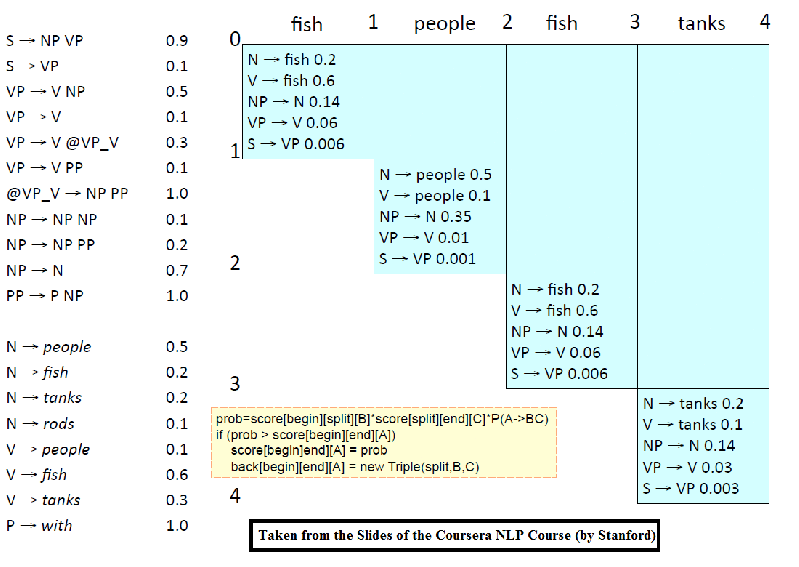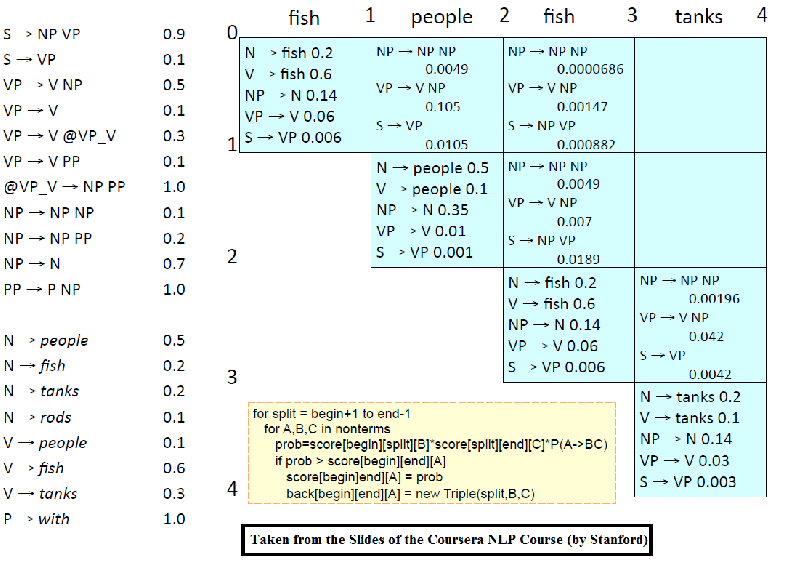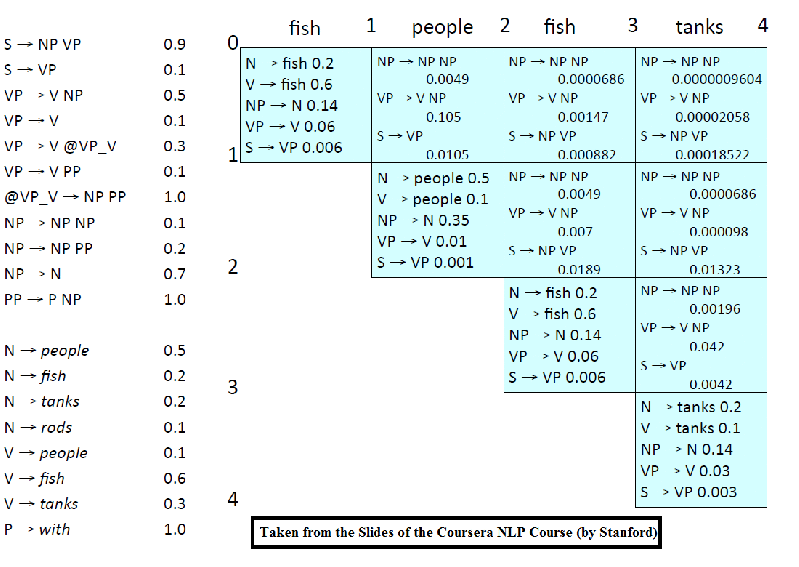
The following animation (prepared from the lecture slides of the same course) shows how the chart for CKY is constructed using dynamic programming for a small set of PCFG grammar.
Evaulation
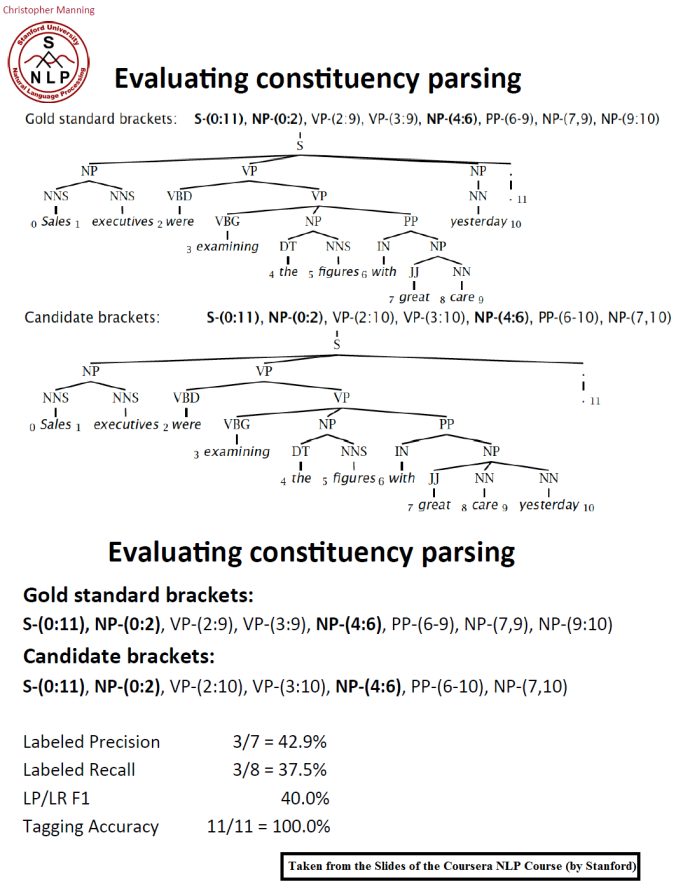
For this assignment we will use your average F1 score to evaluate the correctness of the CKY parser, although in essence we ought to know from the output on the development set (devtest) whether the parser is implemented correctly. The following figure shows an example evaluation:
Results
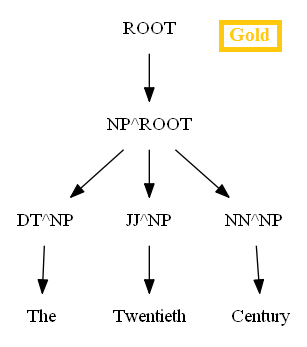
(1) First let’s use a toy minimal training dataset containing just 3 POS-tagged trees, and a dev/test dataset with a single test sentence (with ground-truth), to start with. The following figure shows all the training trees. There are just enough productions in the training set for the test sentence to have an ambiguity due to PP-attachment.

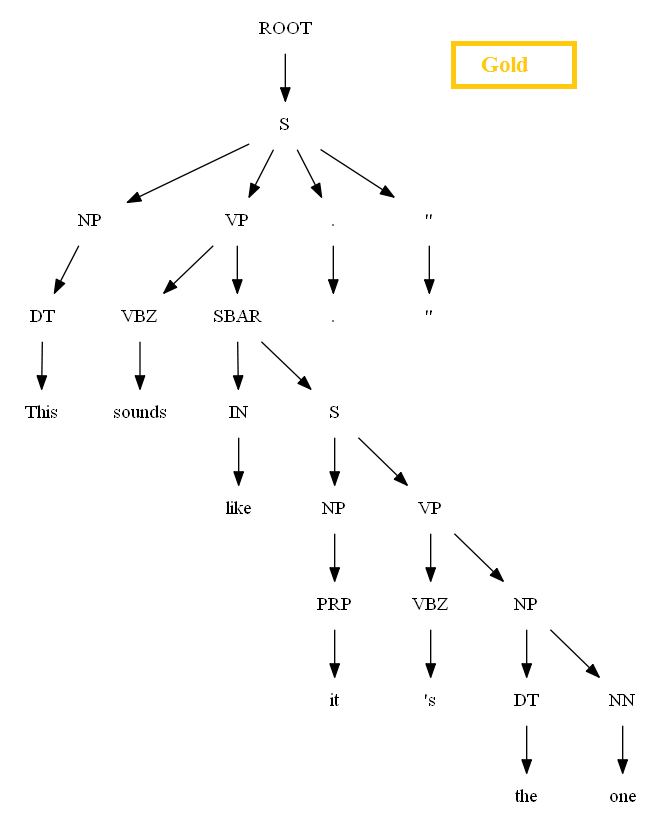
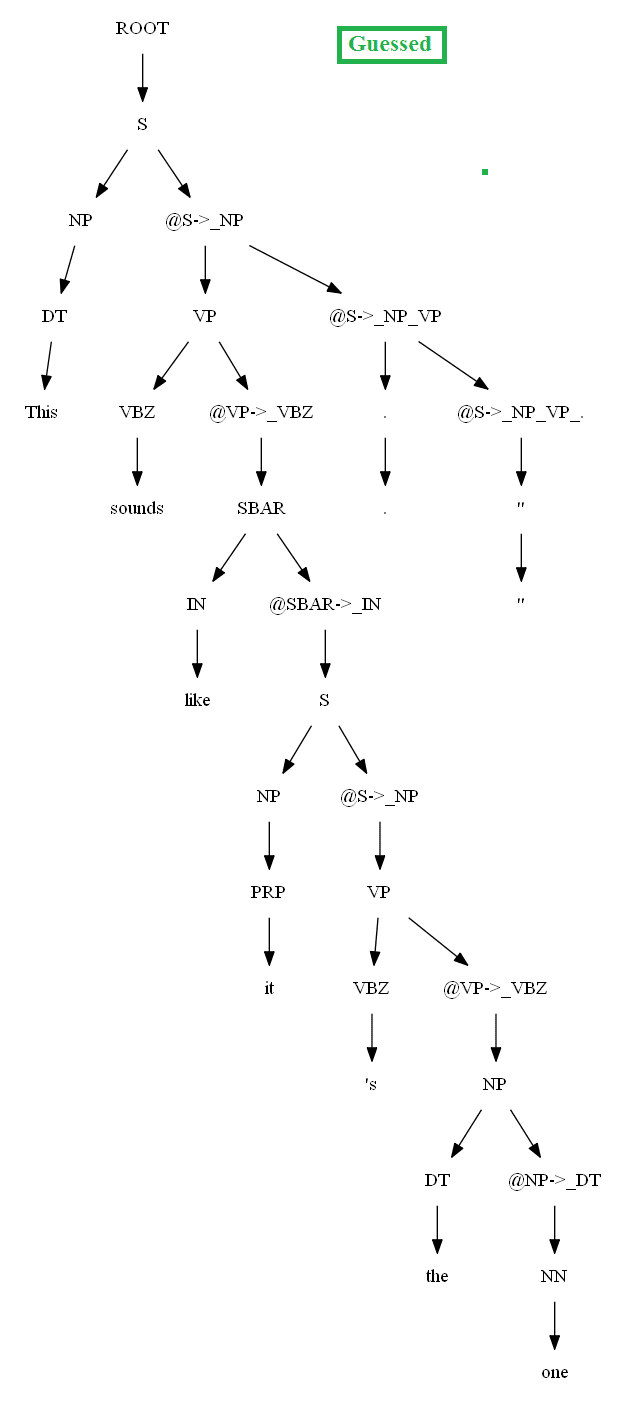
The following figure shows the PCFG learnt from these training trees. Now let’s try to parse a single test sentence‘cats scratch walls with claws’ with the CKY parser and using the PCFG grammar learnt. The following figure shows the manual (gold) parse tree and the best (most probable) parse tree using the CKY dynamic programming algorithm.
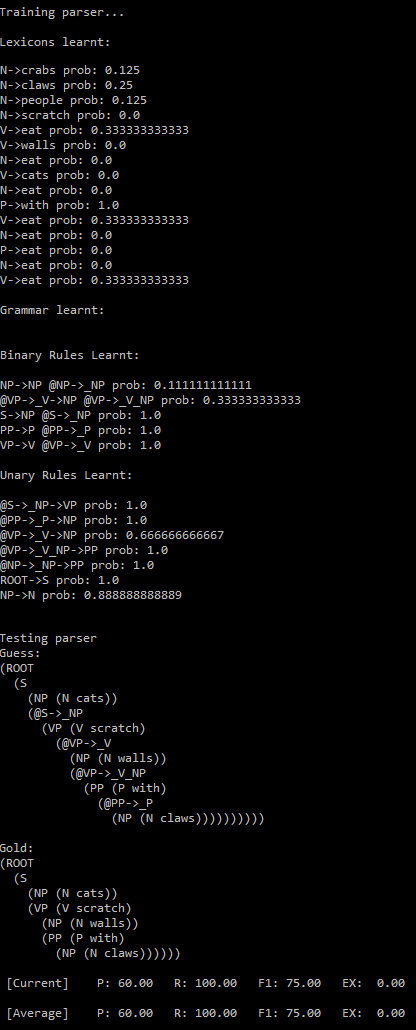
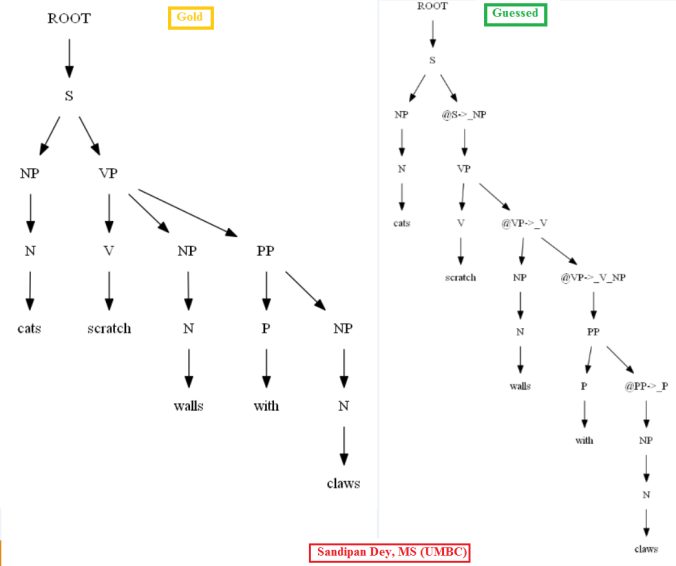
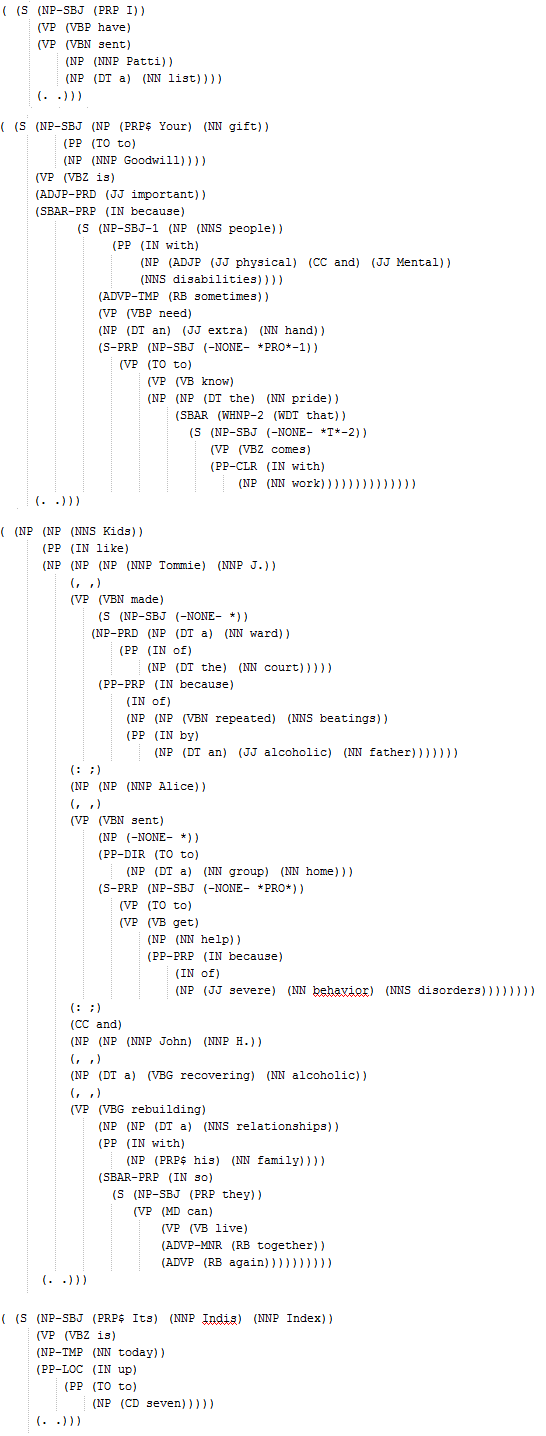
Let’s use all these 3595 POS-tagged training trees to learn the PCFG grammar.
- There are ~10k of lexicon rules producing terminals (with non-zero probabilities) are learnt, some of them are shown below:

- There are ~4.5k binary rules (with non-zero probabilities) producing terminals are learnt, some of them are shown below:

- There are ~3.5k unary rules (with non-zero probabilities) producing terminals are learnt, some of them are shown below:

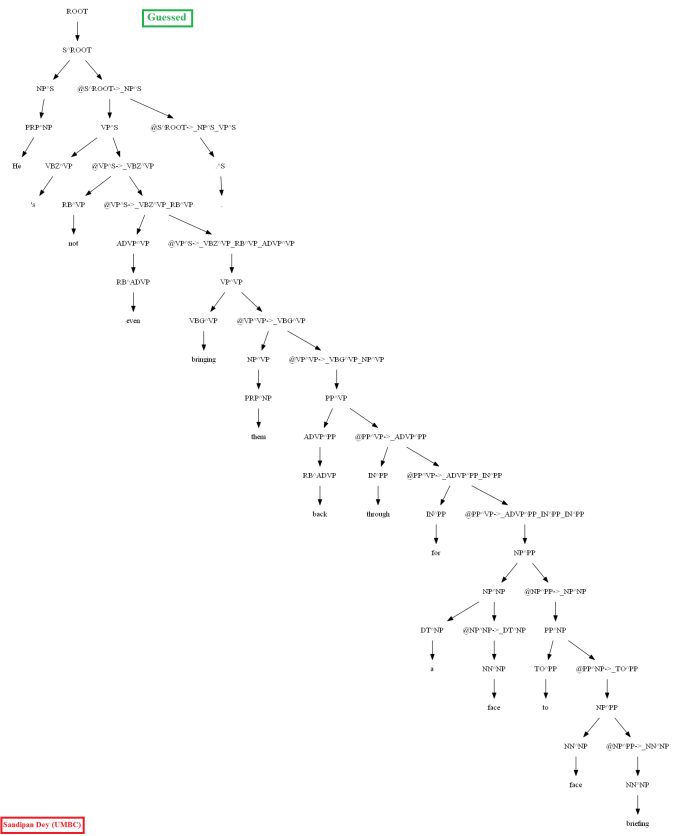
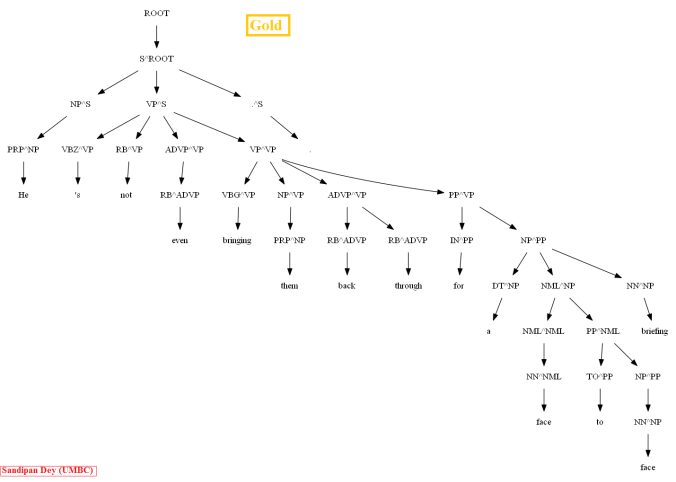
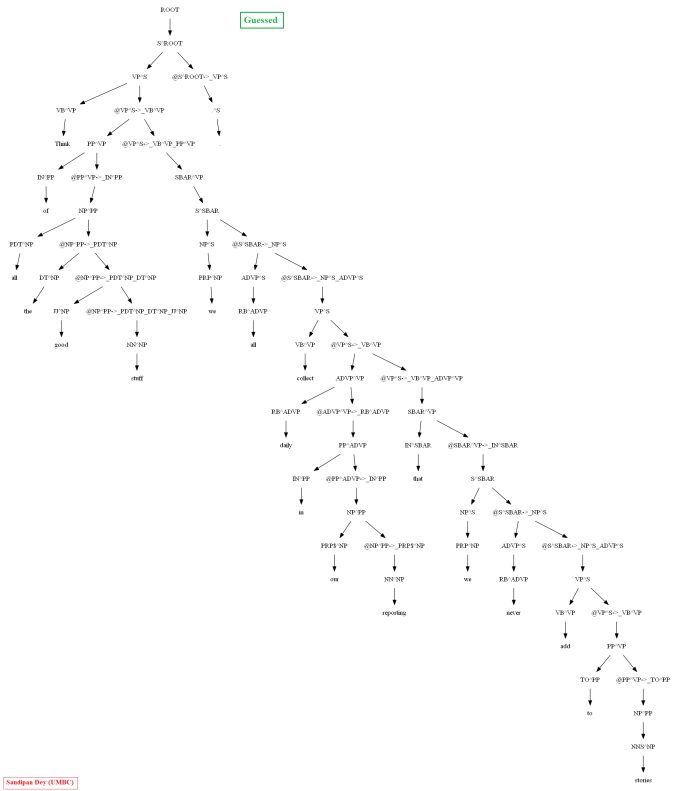
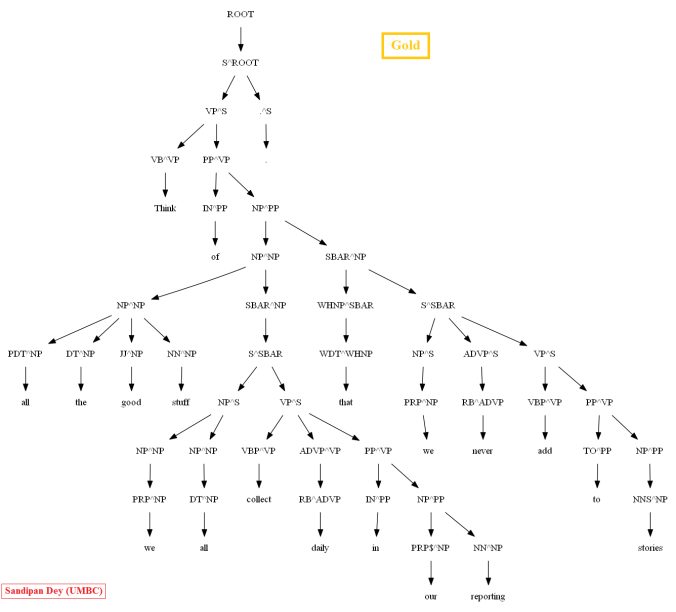
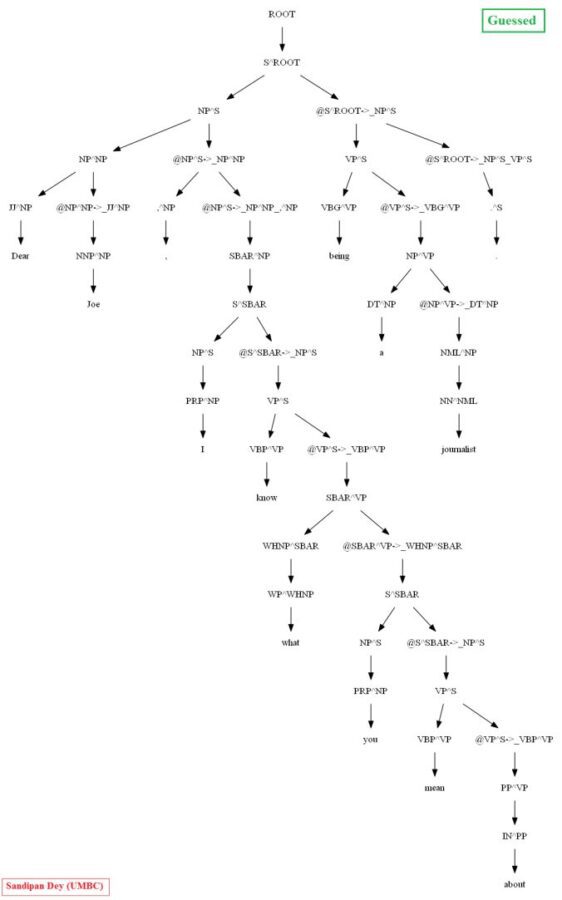
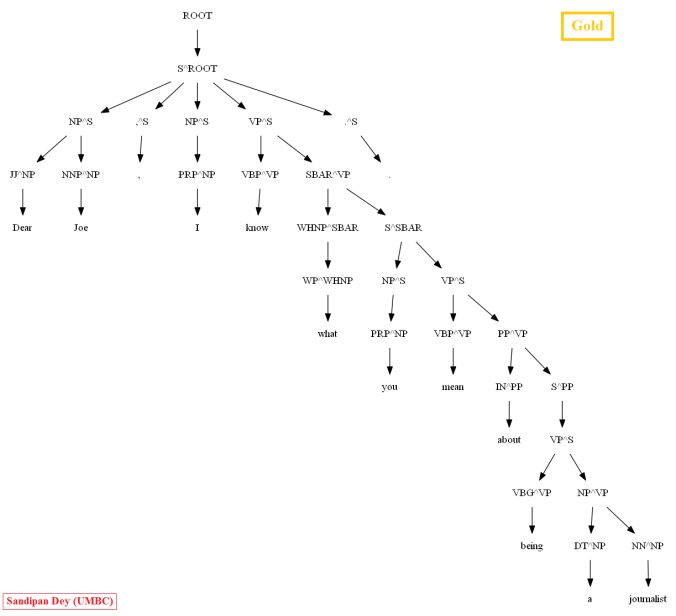
Then let’s evaluate/compare the best parse trees obtained (guessed) with CKY for a few testsentences from the dev/test dataset using the PCFG learnt, with the manually (gold) parsed test trees (there are 355 of them) using precision, recall and F1 score. A few of the test sentence parses are shown in the following figures.
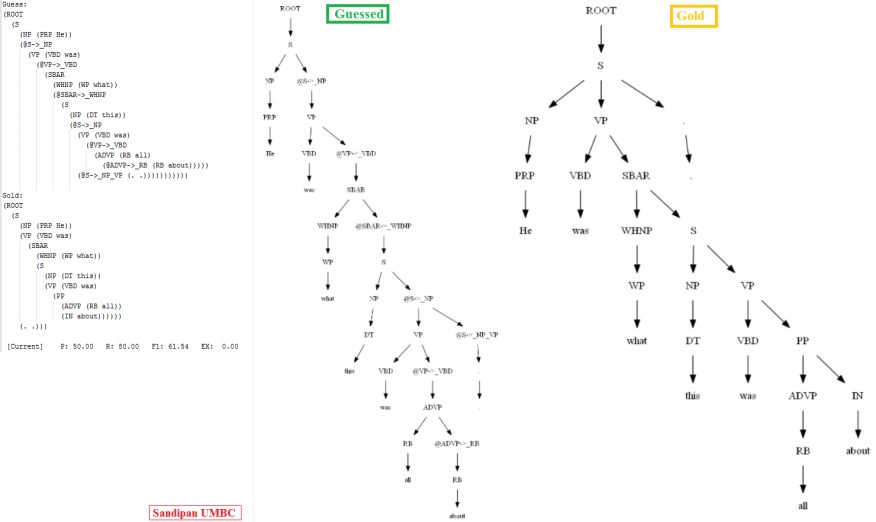
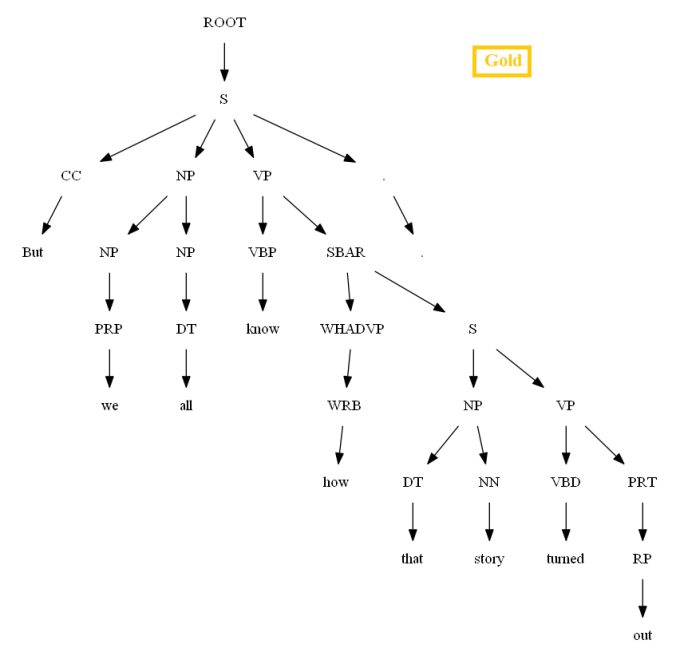
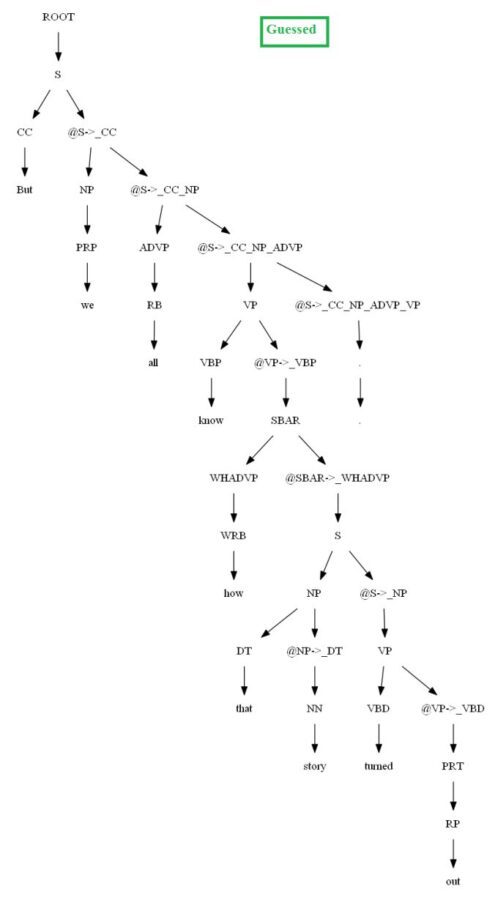
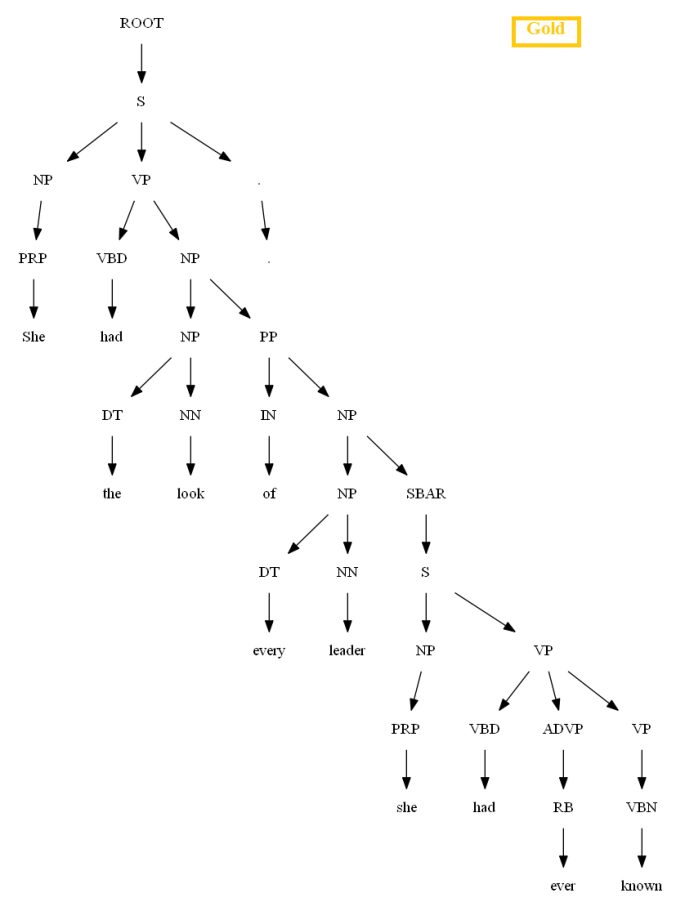
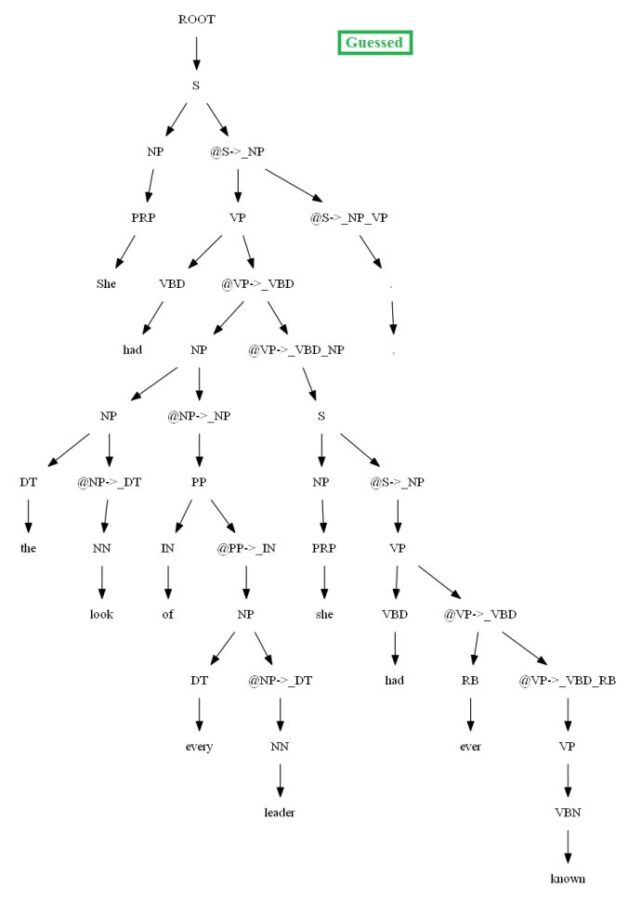
Vertical Markovization
The independence assumptions of a PCFG are ofen too strong. In order to indicate the dependency on the parent non-terminal in a tree the grammar rules can be re-written depending on past k ancestor nodes, denoting the order-k vertical Markovization, as explained in the following figure, which often increases the accuracy of the parse trees.
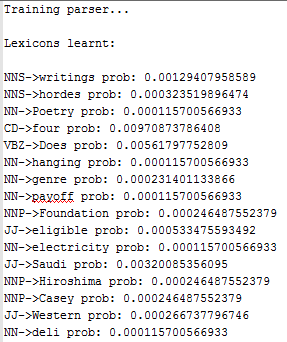
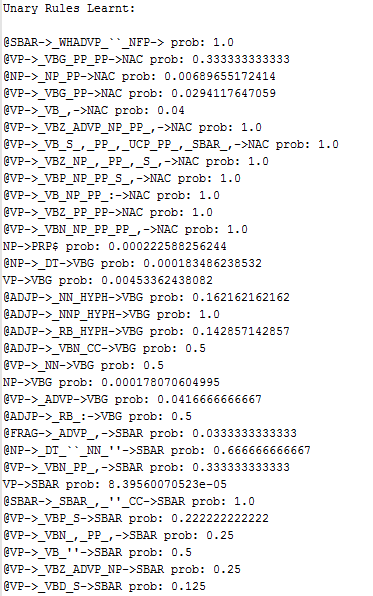
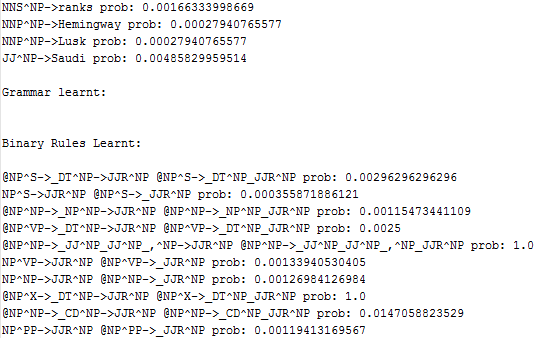
There are ~14k of lexicon rules producing terminals (with non-zero probabilities) are learnt, ~6k binary rules and ~5k unary rules are learnt, some of them are shown below:
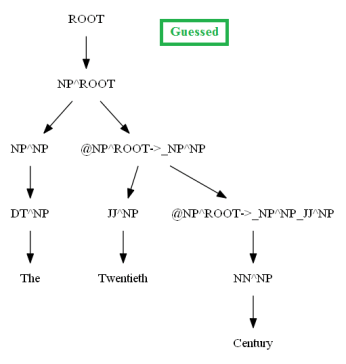
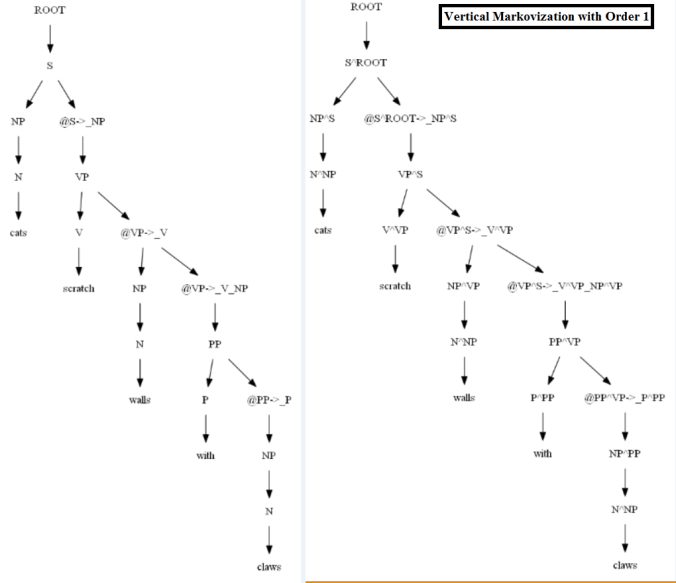
The following figure shows the best parse trees obtained with CKY for a sentence using PCFG learnt with and without vertical Markovization from the minimal dataset.
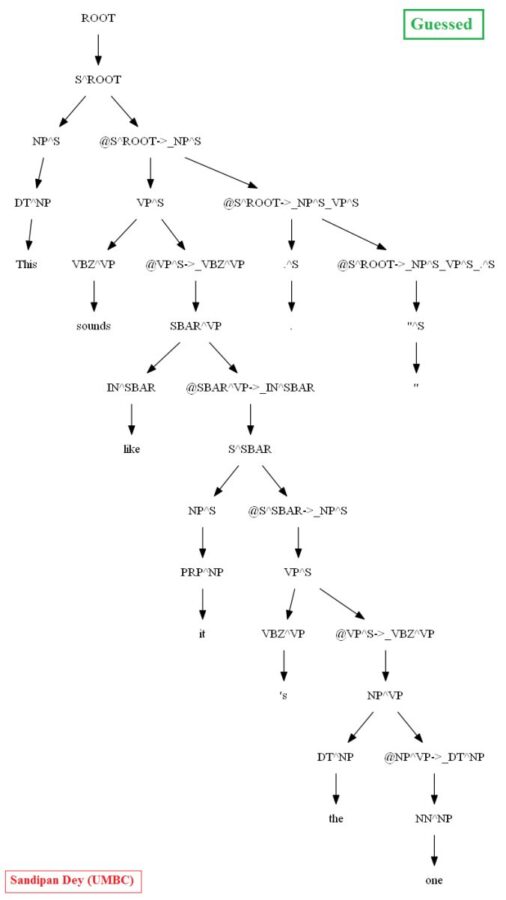
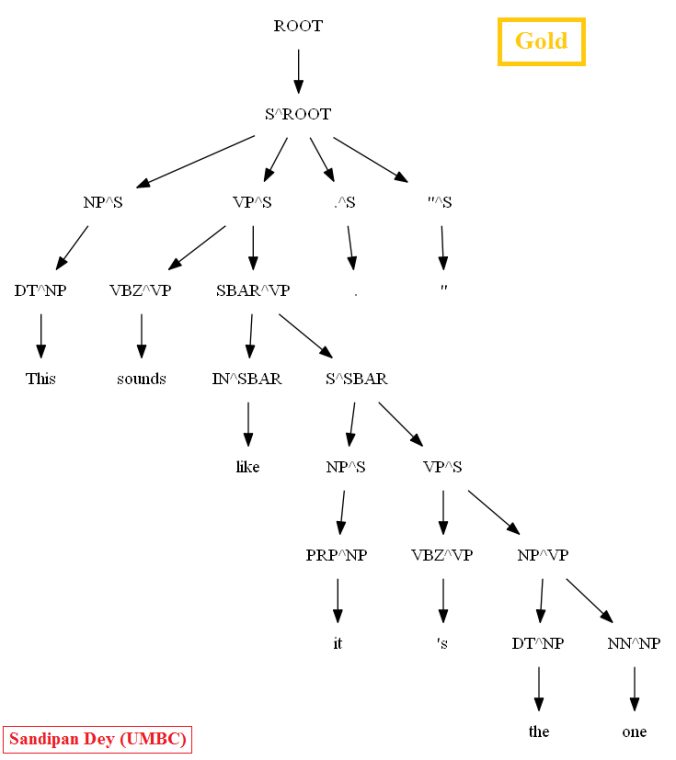
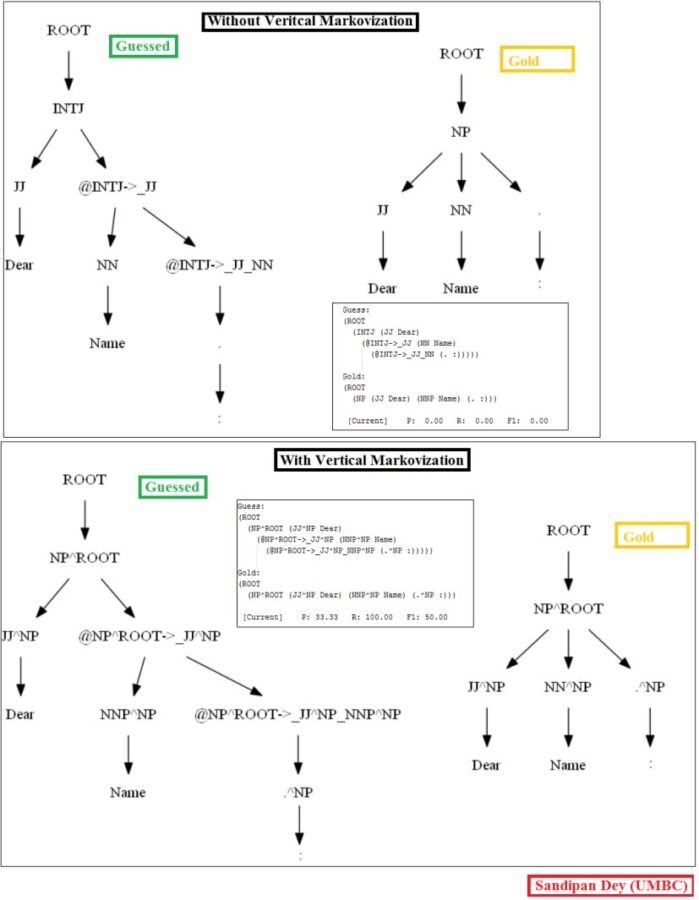
Similarly, using the MASC dataset, as can be seen for the following particular test sentence, the CKY parser performs much better with the PCFG learnt from the Vertically Markovized of the training trees:
A few more parse trees guessed by the CKY using the PCFG learnt from the vertically Markovized training trees are shown below: