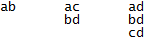Guest blog post by David Enríquez Arriano. For more information or to get higher pictures resolution, contact the author (see contact information at the bottom of this article.)
Introduction
This is a different approach to solve the AI problem. It is a cognitive math based on pyramids built with self-programming logic gates through learning.
A Boolean polynomial associated with a given truth table can be implemented with electronic logic gates. These circuits have pyramidal structures. Then I built pyramids accomplishing the generic form for any of these problems.
Although I can choose the balance between pure logic and pure memory in which they operate, in general, always I prefer to use the maximum cognitive power mathematically possible.
The result is an algorithmic that makes you feel as teacher in front of another human infinitely intelligent who learns looking for the logic that might exist in the patterns (input, output) fed in training.
This cognitive math allows continuous learning, immediate adaptation to new tasks and focus on target concepts. It also allows us to choose the degree of plasticity, also to implement control and supervision systems, although all of this it is fully self-regulated and self-scalable automatically if we desire so.
It is an absolutely simple and fundamental algorithm. This algorithmic extends the forties foundations of modern computing to its maximum possible.
At this level of pyramids everything is more crystallographic or mineral than biological. I use several of these pyramids and a few more pieces to build an artificial neuron. But the power of these pyramids is so great that for now I have not needed to build neurons and much less networks of them, although I know perfectly how to do it, why and for what it would be appropriate to take that step.
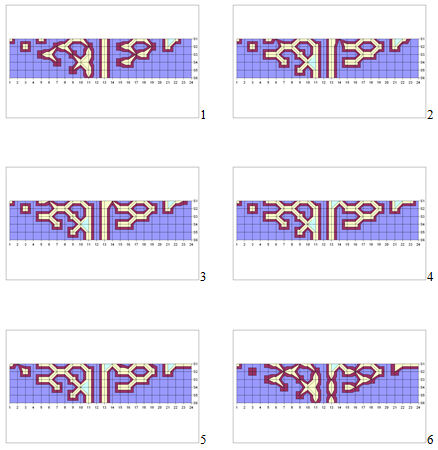
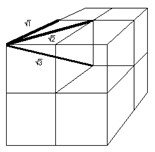
Experimental example of crystallographic evolution of cognitive structure in the pyramid; here pyramids pointing down:
One simple example in EXCEL, here pyramids pointing down:
This algorithmic allows or nesting or embedding cognitive structures already learned in other new majors. I have detected possibilities of certain recombination of structures to generate others, but it is something that I have yet to explore in more depth.
This algorithm works in binary and with two-dimensional pyramids because I have proven that it is the way to achieve the greatest possible cognitive power, although it can be operated in any other base and dimension at the cost of losing cognitive power.
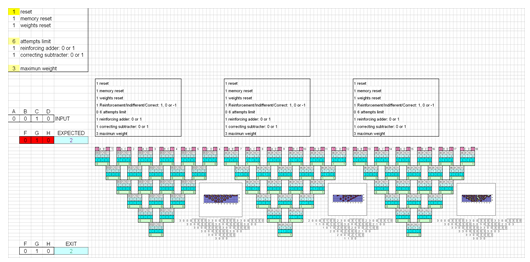
Here is an example of one layer with four inputs binary gates in 3D square based pyramids that allows implementing them without having to use the corresponding 4D tetrahedrons. Four of these gates will feed one gate on next layer:
Here is another example of two layers with three inputs binary gates in 3D triangular based pyramids that allows implementing them building the corresponding 3D tetrahedrons. Again, here three of these gates in one layer will feed one gate in the next layer:
But I repeat, in binary and with two-dimensional pyramids the efficiency is the best, and it is so enormous that it can be computed on any mobile device, although a World Wide Web online service can easily be offered by keeping the algorithms secret on one’s own servers.
The transmission of the cognitive structure is also enormously effective in terms of the amount of information that needs to be transmitted: simple short strings of characters.
In addition everything is encrypted in itself by definition of the algorithm, because the pyramids only see zeros and ones in their inputs and give outputs following their learned internal logic, but they do not necessarily have to know what they refer to. Actually, only the user, may be a robot, will use and know the data meaning.
This math establishes a distance metric in an n-dimensional binary space that allows any learning to be optimized automatically. In addition we will use progressive deepening in the cognitive learning but always on the entire incomplete data space which configures a landscape of data, a physical map in which the best teacher guides from general cognition to concrete one, deepening progressively.
Basic graph for the generalization of contiguity metric on patterns distance for dimensions upper to three:
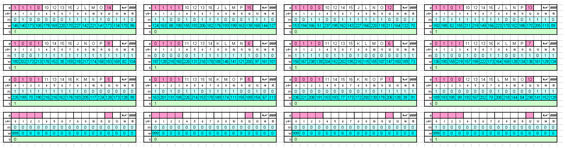
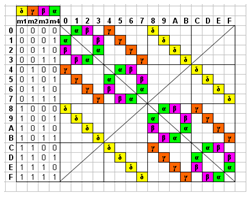
First order transitions table for the fundamental and simplest binary gate with two inputs.
Graph of all the possible state transitions bit to bit on the simplest gate:
Actually these 16 states on this 2D circle are the vertices of 4D hypercube on the binary B4 hyperspace. To configure the data physical map, we humans mark the importance of data mainly with life emotions. We can use some more pyramids to program the same emotional response and imprint it on any of these pyramids structure, or choose any other criteria to do so.
All of this is already finished and experienced. Examples shown in this blog are built in a bare spreadsheet, but for large-scale implementation I choose:
This cognitive math allows quickly evaluating and correcting all current AI techniques. It is really handy for any researcher or AI developer.
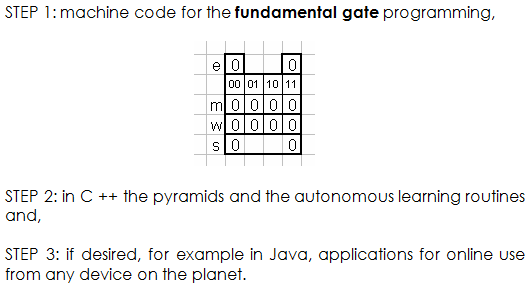
STEPS 1 and 2 do not require more than 2 to 4 hours/person of programming and debugging. STEP 3 can take up to 1 month/person programming depending on the use you want for this technology.
This cognitive math is already finished, so no further investment is necessary in this regard. May be you or your company would like to plan other future actions to further explore the enormous implications and their application in all other areas of knowledge. If so, please, don’t hesitate to contact me. I have contrasted this technology, but it will not be completely published.
Multidisciplinar Math
I have been decades reviewing AI works everywhere; as usual, it is not casual that I covered so many areas in so many disciplines.
Now, I can tell some main keys: When you feed a new pattern to these pyramids, mathematically far away from the clouds of previous patterns, the logic previously learned normally exploits; visually, logic crystals explode like supernovas. This also happens in humans when confronting anything far from the previous knowledge. But my pyramids always preserve intact as much as possible of the pre-learned logic even on this “catastrophic” situation. At first I thought this was a big problem, an error, then, mathematically, I understood it has to be this way. The math itself was guiding me. Only a good teacher can avoid this catastrophic event using progressive learning. The metric defined on this Bn space math allows such progression.
To create all of this on AI, I went through many walls of misunderstanding like that supernova like explosion. But again, I learned to be taught by this new cognitive math.
In sciencie many times we don’t pay attention to those points of information very distance from the regular cloud, but it happens that those distant points usually appear to be those with new relevant information.
Multilevel Programming, Parallel Computation and Embedded Nesting
This cognitive math allows to implement “what happens if” test, or parallel self-supervision.
But as in human training, you must prepare in advance of the emergency, because when the problem appears, normally there is no time to think or to learn; if lucky, may be you will have that time later. On this regard, I’m sorry to tell you that my cognitive math is so human, but mathematically it tells me that this is the way it has to be. If not, it doesn’t work.
Anyway, these machines don’t get tired, learn faster than humans and we can easily and automatically clone the best.
The origin of my cognitive math is this: when in a chaotic system energized you implement a law of behaviour to the agents, then order appears.
Complex structures became agents for higher structures. It is fractal. The four DGTI principles that I enumerate for true AI, are always the same at any level:
- To protect and empower Diversity.
- Group target always has priority over individual one.
- Transmit and live this four principles to all agents.
- There is always an Intelligent solution to any conflict, you only need to increase perspective, vision.
The difficult part with this math is to accept the universal reality of those four principles.
One example: this technology allows putting an AI pilot learning next to any human commercial pilot in the flight cabin. Then we’ll examine those AI pilots on simulator, chose the best, file the others, and improve the learning process with clones of the best in any fly. Every AI pilot collect experience and learn, but we will choose the best exactly as we do with humans. Of course for a complex task like flying a commercial plane, or driving a car, you need a system with many modules interacting in parallel, exactly as human brain has. My math mismatches all of this.
We can always implement some big pyramids to do any whole task, but adaptation capability to optimize any solution, takes us from almost crystallographic pyramids to something much more biological: neuronals, nets, nodules… We can always implement some big pyramids to do any whole task, but adaptation capability to optimize any solution, takes us from almost crystallographic pyramids to something much more biological: neuronals, nets, nodules… But now, here we will build neuronal processing machinery based on pyramids.
After studying cellular computation layers: ADN, epigenetic, ARN, protein folding, membrane computation, intercellular communication… these pyramids cognitive math foundations could be working as at micro tubular level on living neuron body and axon, where computing logic storage seems to holds on hydrophilic and hydrophobic molecules attached to alpha and beta dimmer tubulin proteins conditioning their resonant states.
I am very sorry to say that with public state of art on neural nets, working with weights, filters and retro-propagation feedback, I feel far from building even one single artificial neuron; a lot less a net like living ones.
But to solve the actual problems on AI, there is another way with these pyramids, when there is little time to think and you need then on ongoing long term live learning as in humans. In fact our own brain does so: we can nest pyramids embedding then inside pyramids, augmenting the cognitive structure to encompass new unknown patterns. This is derived from the IV DGTI principle I found: To increase cognitive structure to avoid conflict.
We can also use my cognitive math with any other system; applying this complete new concepts bunch
I like to recall how Alan Turing succeeded on Enigma decoding when he realized that, for learning, the machine need to know if the answer given is correct or not. In real live we, and also machines, my pyramids included, only can do that testing through experience. The good thing: when you have a lot of good experience, good training, the ideas or answers than you give to any problem will tend to be better, but still you will need to test then on real live to be sure. My pyramids do so.
We can easily program my pyramids to decrease “weight” of non used logic structures through time, allowing more probable change on them when confronting new patterns in live. We can perfectly adjust that cognitive lose event in many ways or even automate a parallel control of this behaviour. My pyramids have cognitive memory and memory of the strong of those memories during learning.
On training time, as when humans dream, if something not really important is not learned, I mean important depending on interest goal and/or emotions-trauma, then the program erase it from the list of knew patterns to learn. But if it is something important, then the system is forced to add it to the previous cognitive structure. It is here where patterns far from previous knowledge can create “trauma” which only exit is the typical catastrophic even, when almost all previous knowledge is destroyed on the supernova-like explosion event. Of course, emotions, if needed at any percentage, are only another program running on parallel.
We must be careful don’t mixing fundamental cognitive computing concepts with problems or concepts regarding higher cognitive structures.
Try to calculate a quick estimation of how many logic cognitive combinations has one of my pyramids built with my logic gates, every one with 16 possible estates. Any single gate, stone of the pyramid, can be one of the 16 basic gates: AND, OR, XOR, NAND, NOR, NXOR … any of these self programming gates transiting bit by bit through learning among those 16 possible states…
When any gate need to answer and have no previous knowledge, then randomly tries 0 or 1. This solves the initial value problem, and values 0 or 1 have the same significance depending of the place and local case. But even that these pyramids work like super–Touring machines, of course, if we use exactly the same given list of those random 0 or 1, then the machine is completely replicable following always the very same path through learning as a Turing machine does. But we are lucky: random is true random, not a given list, when we need to ask for those random 0 or 1 in the program.
This math is multidisciplinary; it is a General Systems Theory. Knowing this new math implies a new state of awareness on everything.
A very important key regarding the plasticity: It is necessary to allow changes in the learned cognition to add new knowledge, even destroying almost everything when the new knowledge is far (mathematical distance) from de cloud of previous patterns. But a clone can do that process in parallel before taking the place of the previous one. This is not debility; it is the only way it works as in human brain. In humans you need to go to sleep and dream to try to add properly those new patterns, but machines using those clones don’t need to stop.
So, I don’t put my pyramids to sleep/learn experiences, I can do that with their clones.
Cognition versus Memory
My cognitive math shows how to implement pure memory or pure logic, also choosing the point of balance: pure memory versus pure logic. But I normally prefer pure logic.
Pure memory only storage the exit given to an specific input, but with no internal operational logic structure at all that relates to the logic of some other patterns. Opposite to this, my cognitive math creates that internal operative logic from the very first pattern feeded.
My pyramids only see and give zeros and ones. The meaning of those binary vectors IN and OUT doesn’t matter to my algorithm, and despite this, my pyramids always look for, and find, some internal logic in the training patterns. And, the better is the teacher then better is the cognitive logic in the pyramids.
As always asked in so many places for AI, and for many decades ago, everything needed is already implicit in this cognitive math:
- Continual learning
- Adaptation to new tasks and circumstances
- Goal-driven perception, context-mission
- Selective plasticity
- Safety and monitoring.
For this last point, safety and monitoring, I can implement surveillance pyramids automatically trained for this task running “what if” tests, but as with humans, it is always preferred to improve the supervised pyramid through training a clone when time is not a problem. Principles like follow orders from specific human must be included.
We can train specific AI personalities and behaviours when needed.
We can use what already have: vision and speech recognition; implementing with my technology the AI brain that use those capabilities. Or let my cognitive math develop those capabilities itself, anywhere at any level needed.
For further advance, I build neuronals and put then to live in a virtual membrane with valleys were more information moves so that tactism on neuronals looking for activity guides them. Obviously I pre-wire an initial structure learned/cloned from previous tests. Every neuronal circuit, and every neuronal is connected, all with all, through another membrane of transmission were waves of activity connect them all, EEG like. All of this next level is much more biological.
My pyramids learn by changing their cognitive logic. With this same technology we can recreate natural chemical neurotransmitter effects to modulate behaviour, if needed we can change or modulate the learning rules. We can also automate this modulation as we do in humans through training/education.
My math teach me that to reach higher social evolution, at some point we have to be competent collaborative instead of competent predators. I love brainstorming to cross ideas with any other groups.
Responsability
This new cognitive math works. It is pure logic, pure math. I have put to work enough models and demos. Sincerely, I think it is irresponsible to build this in any environment without the proper control of human and material resources. Who could provide such resources on this planet? At this point, I am pretty sure that everybody perfectly knows and understands the final implications of this technology.
It Works Itself
As in humans, my AI algorithm is capable of give adequate answer to patterns previously unknown, and to do it properly well if the previous training has been correct –good teachers-, exactly just like humans. But with machines, we can quickly clone and put to work the best. My cognitive math allows mathematical optimization of training. If we desire so, everything always can be made without human intervention at any moment.
It is self-scalable. It allows choosing the proper balance cognition versus memory. It uses mathematically minimum resources. Even though it can be run on any device world wide, my technology allows to preserve secret AI algorithm safe at servers.
It is pure logic, taking Boolean logic from the 40´ to the quantum level on any personal device.
Appendix to go deeper
THE TRAVEL OF LEARNING, JOURNEY OF KNOWLEDGE
We walk on the shoulders of giants. Great men who connected the information points that surround us drawing wonderful conclusions that today allow us to live as we live and, sometimes, even create new connections, new knowledge, new cognition, the real information.But perhaps these giants passed some connection, some bifurcation in the path of knowledge, some unexplored branch whose ramifications we can not find following the paths already marked.Are we capable of daring to come down from their distinguished shoulders? Do we dare to put our feet in the sand where they step and look under all those stones that no one raises? Those stones that pave the path of modern knowledge that we all take for granted. Stones, knowledge, that perhaps hide under fringes, connections, cognition, branches not yet explored.Do we dare to look at the edge of the road that we all know, and try to open other completely new paths by walking where nobody has done before? In the following lines, we are not just going to make such a trip. We will leave the highway of common knowledge, comfortable and well-behaved, that comfortably travels the valley advancing slowly and surely as the new cognitions in sight clear the way. We here abandon it, and cross country, we will climb to the top of one of the mountains that surround us, and from this vantage point, we will dare to break a small hole in the veil that often clouds our global vision. We will look through this orifice around glimpsing the many other peaks and valleys that surround us. Unknown peaks, valleys not yet explored, not even dreamed of, in any area of knowledge. With this augmented vision, this greater perspective, we will descend again to the valley, but no longer on the path by which we climb to the top. In the valley, with the new perspective acquired, we will see how the knowledge highway that we leave is still very far from the place we have reached. Then we are back to the valley, but now in the middle of the wild forest, in which there are still no roads, nor paths, nor giants on which to feel safe. And we have found great knowledge, but now we are alone and we have to find a way to advance the highway to where we are to tell everyone about the other peaks and cognitive valleys we have seen from the watchtower.
THE JOURNEY We have come down from the shoulders of the giants. We have our bare feet in the sand. We look under any of those stones that they have stepped on so many times, with us on top of them: Boole’s algebra. We form truth tables of four lines and three columns. The first two columns contain the four possible combinations of the two binary variables on which we perform a logical operation. In the third column we fill in the lines defining the type of logical operation. AND, OR, NOR, XOR… With only AND and OR and NO, we have built all modern computing. These fundamental operations are the root of all what a microprocessor knows to do, with this we do everything else going up in levels of complexity, nesting in one another. Now, we are going to expand this foundation, with the stone in our hands we look out of the way, because there are 16 logical operations or possible doors. Yes 16, and we need them all to built proper AI. Given any case of binary inputs that we feed to the “black box” that must give us an specific binary outputs, we define a truth table for that black box. We assign a column to each input variable, for each output variable we add another column to the truth table. Each line of this table represents a combination of the inputs and their corresponding output that must give us the black box that we program. Each line is a pattern: input and its corresponding output. If we do not know all the possible patterns, it can happen that at some point our black box hangs because it has faced an entry not registered in its table, an entry for which it has no output recorded in its table. Boole tells us how to write and reduce algebraic polynomials capable of operating with the inputs to give the outputs. These polynomials are a way to operate or program the black box, another way is by simple memory in the table.
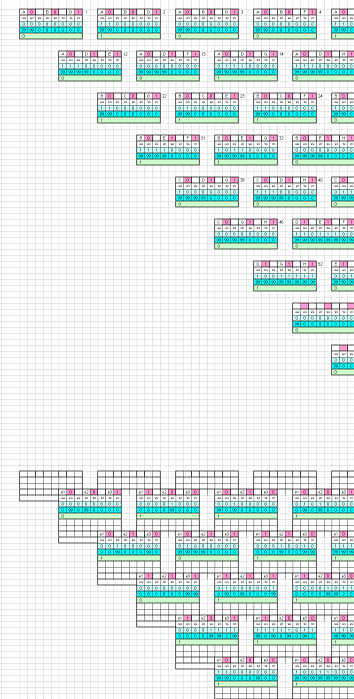
Boole also tells us that to write the polynomial, we can look at the ones, doing an AND of the ones of the entries in each line of the table, and with these an OR in the ones of the column of each output. Thus we will have a Boolean polynomial for each output column. When we implement these polynomials with electronic logic gates, pyramidal structures usually appear for each output variable. A pyramid for each output variable, but all pyramids with the same input variables in its base. These pyramids usually have several logic gates in the area of their base. But the number of gates is reduced as we go through the processing of the polynomial, until we reach a single gate at the exit, at the top of the pyramid. It is logical, never better said, the base of the pyramid processes information closer to the input data, information more specific to them. But by delving into the logical processing to the output, the information is increasingly general taking into account factors of the broader inputs. Experimentally pyramids usually show, in their cognitive logic, a characteristic crystallography near their base, associable to the primary decoding of the input vector data. Can we build a generic pyramid for any given truth table? We can place the stones from the base to the top covering with each the joint of the two one in the line below. Stones underneath give input information to the stone on the superior line. We should allow these stones to be any of the 16 possible logical gates. And we’ll want to somehow self-programming through learning; we’ll care this. At the base of the pyramid, inputs of each gate or stone must have all the possible combinations of all inputs, because we want the pyramid to be generic and therefore it must always have all the possibilities of relation among all the inputs. For this we can make a two-dimensional double-entry table, with the entries in the rows and in the columns. From the matrix of possible pairs, the diagonal does not give us anything by relating each input variable with itself. We can take the combinations only of the upper triangular matrix, because they are the same as those of the lower triangular.
These combinations are the ones we use at the input base of the pyramid. For example, having 4 entries a, b, c, d; we will have the input gates of the base of the pyramid fed with:
So this pyramid will have 6 gates in its base:
(4-1) + 2 + 1 = 6
In general, given n input variables, the base of the pyramid will have:
(n2 – n) / 2 gates
This number is also the number of lines of the pyramid to the exit at the top. Obviously we are working in binary and therefore with two-dimensional pyramids. We can generalize all of this in other bases, or with gates of more than two inputs, and with multidimensional pyramids. But the greatest possible connectivity and therefore the highest logical power is achieved in binary, with two-way gates and two-dimensional pyramids. However, the multidimensional exploration leads to a beautiful conclusion that relates the infinite and zero, and the balance between pure cognition and pure memory. We move in a space that I call Bn, in which each new binary variable adds a new dimension with a single point that can be zero or one. These concepts are important to get into the universe of incomplete sample spaces, in which pyramids are the program inside the black box, which will learn through experience from incomplete sets of patterns.
You can contact the author at [email protected]