Introduction
Almost every machine learning algorithm comes with a large number of settings that we, the machine learning researchers and practitioners, need to specify. These tuning knobs, the so-called hyperparameters, help us control the behavior of machine learning algorithms when optimizing for performance, finding the right balance between bias and variance. Hyperparameter tuning for performance optimization is an art in itself, and there are no hard-and-fast rules that guarantee best performance on a given dataset. In Part I and Part II, we saw different holdout and bootstrap techniques for estimating the generalization performance of a model. We learned about the bias-variance trade-off, and we computed the uncertainty of our estimates. In this third part, we will focus on different methods of cross-validation for model evaluation and model selection. We will use these cross-validation techniques to rank models from several hyperparameter configurations and estimate how well they generalize to independent datasets.
Table of contents
- About Hyperparameters and Model Selection
- The Three-Way Holdout Method for Hyperparameter Tuning
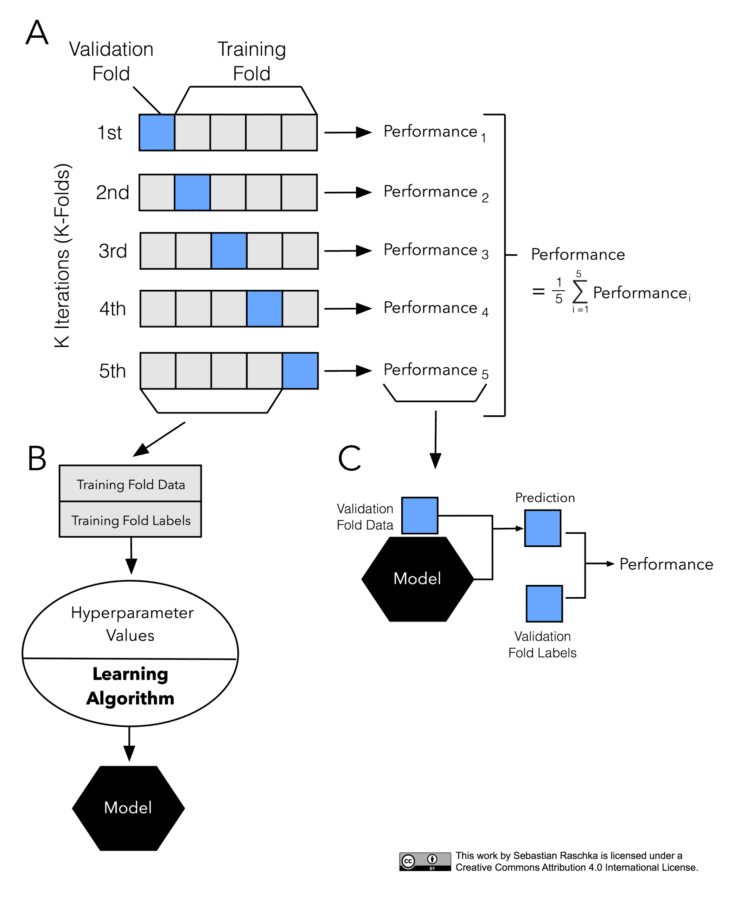
- Introduction to K-fold Cross-Validation
- Special Cases: 2-Fold and Leave-One-Out Cross-Validation
- K and the Bias-variance Trade-off
- Model Selection via K-fold Cross-validation
- The Law of Parsimony
- Summary and conclusion
- What’s Next
To read the whole article, with each point all explained and illustrated, click here.