Long title: Measuring Semantic Relatedness using the Distance and the Shortest Common Ancestor and Outcast Detection with Wordnet Digraph in Python
The following problem appeared as an assignment in the Algorithm Course (COS 226) at Princeton University taught by Prof. Sedgewick. The description of the problem is taken from the assignment itself. However, in the assignment, the implementation is supposed to be in java, in this article a python implementation will be described instead. Instead of using nltk, this implementation is going to be from scratch.
The Problem
- WordNet is a semantic lexicon for the English language that computational linguists and cognitive scientists use extensively. For example, WordNet was a key component in IBM’s Jeopardy-playing Watson computer system.
- WordNet groups words into sets of synonyms called synsets. For example, { AND circuit, AND gate } is a synset that represent a logical gate that fires only when all of its inputs fire.
- WordNet also describes semantic relationships between synsets. One such relationship is the is-a relationship, which connects a hyponym (more specific synset) to a hypernym (more general synset). For example, the synset { gate, logic gate } is a hypernym of { AND circuit, AND gate } because an AND gate is a kind of logic gate.
- The WordNet digraph. The first task is to build the WordNet digraph: each vertex v is an integer that represents a synset, and each directed edge v→w represents that w is a hypernym of v.
- The WordNet digraph is a rooted DAG: it is acyclic and has one vertex—the root— that is an ancestor of every other vertex.
- However, it is not necessarily a tree because a synset can have more than one hypernym. A small subgraph of the WordNet digraph appears below.
The WordNet input file formats
The following two data files will be used to create the WordNet digraph. The files are in comma-separated values (CSV) format: each line contains a sequence of fields, separated by commas.
- List of synsets: The file synsets.txt contains all noun synsets in WordNet, one per line. Line i of the file (counting from 0) contains the information for synset i.
- The first field is the synset id, which is always the integer i;
- the second field is the synonym set (or synset); and
- the third field is its dictionary definition (or gloss), which is not relevant to this assignment.
For example, line 36 means that the synset {
AND_circuit,AND_gate} has an id number of 36 and its gloss isa circuit in a computer that fires only when all of its inputs fire. The individual nouns that constitute a synset are separated by spaces. If a noun contains more than one word, the underscore character connects the words (and not the space character).
- List of hypernyms: The file hypernyms.txt contains the hypernym relationships. Line i of the file (counting from 0) contains the hypernyms of synset i.
- The first field is the synset id, which is always the integer i;
- subsequent fields are the id numbers of the synset’s hypernyms.
For example, line 36 means that synset 36 (
AND_circuit AND_Gate) has 42338 (gate logic_gate) as its only hypernym. Line 34 means that synset 34 (AIDS acquired_immune_deficiency_syndrome) has two hypernyms: 47569 (immunodeficiency) and 56099 (infectious_disease).
The WordNet data type
Implement an immutable data type WordNet with the following API:
- The Wordnet Digraph contains 76066 nodes and 84087 edges, it’s very difficult to visualize the entire graph at once, hence small subgraphs will be displayed as and when required relevant to the context of the examples later.
- The sca() and the distance() between two nodes v and w are implemented using bfs (bread first search) starting from the two nodes separately and combining the distances computed.
Performance requirements
- The data type must use space linear in the input size (size of synsets and hypernyms files).
- The constructor must take time linearithmic (or better) in the input size.
- The method
isNoun()must run in time logarithmic (or better) in the number of nouns. - The methods
distance()andsca()must make exactly one call to thelength()andancestor()methods inShortestCommonAncestor, respectively.
The Shortest Common Ancestor
- An ancestral path between two vertices v and w in a rooted DAG is a directed pathfrom v to a common ancestor x, together with a directed path from w to the same ancestor x.
- A shortest ancestral path is an ancestral path of minimum total length.
- We refer to the common ancestor in a shortest ancestral path as a shortest common ancestor.
- Note that a shortest common ancestor always exists because the root is an ancestor of every vertex. Note also that an ancestral path is a path, but not a directed path.
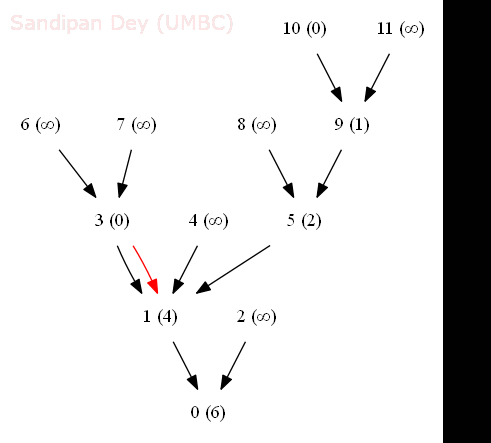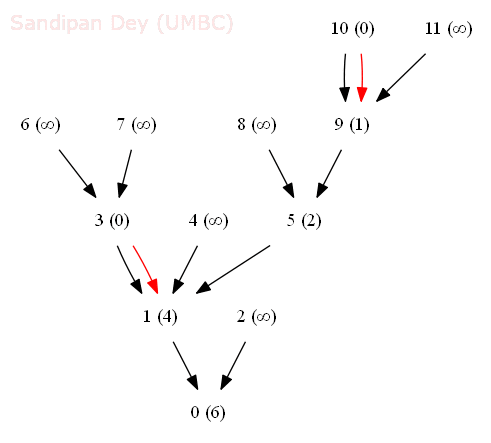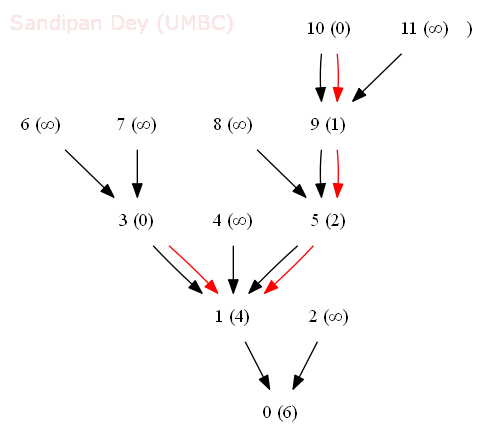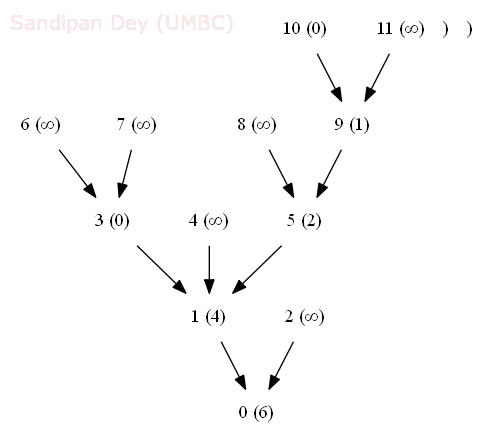
- The following animation shows how the shortest common ancestor node 1 for thenodes 3 and 10 for the following rooted DAG is found at distance 4 with bfs, along with the ancestral path 3-1-5-9-10.

- We generalize the notion of shortest common ancestor to subsets of vertices. A shortest ancestral path of two subsets of vertices A and B is a shortest ancestral path over all pairs of vertices v and w, with v in A and w in B.
- The figure (digraph25.txt) below shows an example in which, for two subsets, red and blue, we have computed several (but not all) ancestral paths, including the shortest one.

Shortest common ancestor data type
Implement an immutable data type
ShortestCommonAncestorwith the following API:
Basic performance requirements
The data type must use space proportional to E + V, where E and V are the number of edges and vertices in the digraph, respectively. All methods and the constructor must take time proportional to E+ V (or better).
Measuring the semantic relatedness of two nouns
Semantic relatedness refers to the degree to which two concepts are related. Measuring semantic relatedness is a challenging problem. For example, let’s consider George W. Bushand John F. Kennedy (two U.S. presidents) to be more closely related than George W. Bush and chimpanzee (two primates). It might not be clear whether George W. Bush and Eric Arthur Blair are more related than two arbitrary people. However, both George W. Bush and Eric Arthur Blair (a.k.a. George Orwell) are famous communicators and, therefore, closely related.
Let’s define the semantic relatedness of two WordNet nouns x and y as follows:
- A = set of synsets in which x appears
- B = set of synsets in which y appears
- distance(x, y) = length of shortest ancestral path of subsets A and B
- sca(x, y) = a shortest common ancestor of subsets A and B
This is the notion of distance that we need to use to implement the distance() and sca() methods in the WordNet data type.
Finding semantic relatedness for some example nouns with the shortest common ancestor and the distance method implemented
apple and potato (distance 5 in the Wordnet Digraph, as shown below)
As can be seen, the noun entity is the root of the Wordnet DAG.
beer and diaper (distance 13 in the Wordnet Digraph)
beer and milk (distance 4 in the Wordnet Digraph, with SCA as drink synset), as expected since they are more semantically closer to each other.
bread and butter (distance 3 in the Wordnet Digraph, as shown below)
cancer and AIDS (distance 6 in the Wordnet Digraph, with SCA as disease as shown below, bfs computed distances and the target distance between the nouns are also shown)
car and vehicle (distance 2 in the Wordnet Digraph, with SCA as vehicle as shown below)

cat and dog (distance 4 in the Wordnet Digraph, with SCA as carnivore as shown below)
cat and milk (distance 7 in the Wordnet Digraph, with SCA as substance as shown below, here cat is identified as Arabian tea)
Einstein and Newton (distance 2 in the Wordnet Digraph, with SCA as physicist as shown below)
Leibnitz and Newton (distance 2 in the Wordnet Digraph, with SCA as mathematician)
Gandhi and Mandela (distance 2 in the Wordnet Digraph, with SCA as national_leader synset)
laptop and internet (distance 11 in the Wordnet Digraph, with SCA as instrumentation synset)
school and office (distance 5 in the Wordnet Digraph, with SCA as construction synset as shown below)
bed and table (distance 3 in the Wordnet Digraph, with SCA as furniture synset as shown below)

Tagore and Einstein (distance 4 in the Wordnet Digraph, with SCA as intellectual synset as shown below)
Tagore and Gandhi (distance 8 in the Wordnet Digraph, with SCA as person synset as shown below)
Tagore and Shelley (distance 2 in the Wordnet Digraph, with SCA as author as shown below)

text and mining (distance 12 in the Wordnet Digraph, with SCA as abstraction synset as shown below)

milk and water (distance 3 in the Wordnet Digraph, with SCA as food, as shown below)
Outcast detection
Given a list of WordNet nouns x1, x2, …, xn, which noun is the least related to the others? To identify an outcast, compute the sum of the distances between each noun and every other one:
di = distance(xi, x1) + distance(xi, x2) + … + distance(xi, xn)
and return a noun xt for which dt is maximum. Note that distance(xi, xi) = 0, so it will not contribute to the sum.
Implement an immutable data type Outcast with the following API:
Examples
As expected, potato is the outcast in the list of the nouns shown below (a noun with maximum distance from the rest of the nouns, all of which except potato are fruits, but potato is not). It can be seen from the Wordnet Distance heatmap from the next plot, as well as the sum of distance plot from the plot following the next one.

Again, as expected, table is the outcast in the list of the nouns shown below (a noun with maximum distance from the rest of the nouns, all of which except table are mammals, but table is not). It can be seen from the Wordnet Distance heatmap from the next plot, as well as the sum of distance plot from the plot following the next one.
Finally, as expected, bed is the outcast in the list of the nouns shown below (a noun with maximum distance from the rest of the nouns, all of which except bed are drinks, but bed is not). It can be seen from the Wordnet Distance heatmap from the next plot, as well as the sum of distance plot from the plot following the next one.