The Entropy is one of the most important concepts in many fields like physics, mathematics, information theory, etc.
Entropy is related to the number of states that one stochastic system can take and how this system will evolve with time, in such a way that the uncertainty will be maximized.
This will happened y two ways, first, every system will choose the configuration with a higher degree of entropy among all that are available and second, if we let the system evolve, after some time it will be in a configuration with a higher entropy than the initial value.
We define the entropy as the logarithm of number of states that are available for the system.
The number of states available for one system is given by the probabilities of each one of these states, so it looks reasonable to think in a definition based on these probabilities.
We also ask this function to compliant some restrictions:
The sum of probabilities of the available states must equals 1
The entropy of a system made by two subsystems must be the sum of the entropies of these subsystems
These requirements will force the entropy function to be consistent either if we look at the system as hole or we look at it as the sum of two subsystems 1 and 2. Thus
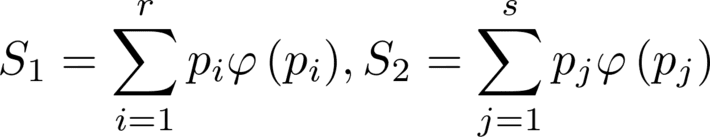
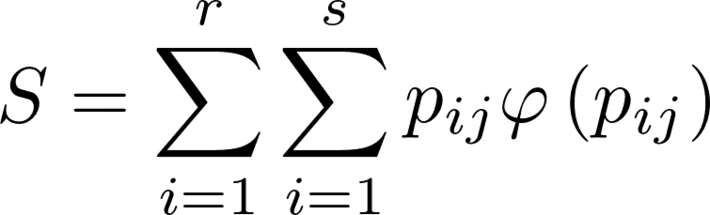
So, we find that
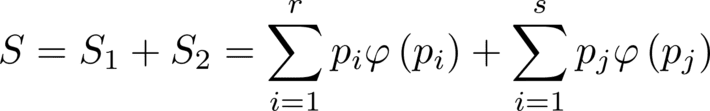
The only function that can maintain the relationship is the so we introduce the definition of entropy as a function of the probabilities of the states in this way.
Now that we have an entropy function that we can manage, let’s think of a system that can take different states with different probabilities.
One example that familiar and easy to analyze is a rolling dice.
One dice has 6 faces with values (1,2,3,4,5,6) and a uniform distribution of probability 1/6 for every value, so the entropy for one dice is given by =1.792
If we increase the complexity of the system introducing mode dices, n=2, n=3, n=4, etc., the entropy of the system will be sum of them = (1.792·n)
For example, using R, we calculate possible combinations for two dices:
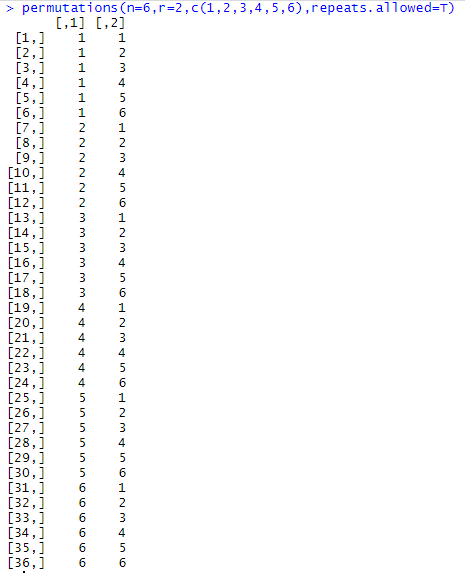
We are interested in seeing what happens if consider the dices indistinguishable and what happens to the entropy in this case. This situation may occur when we do not have direct access to the states, but to a function of them (sometimes called observable), to illustrate this, we will consider the sum of the values of the n dices used in every draft.
Considering the states given by the observable “sum”, we will observe a dramatical change in the probability distribution and entropy. Now the state (2,1) and (1,2) will be the same state because both sum 3, (6,1), (4,3), (3,4), (4,3), (2,5), (5,2) and (1,6) will be the same state because they sum 7 and so on.
To calculate the new states and new probabilities of the system we use a numerical approach.
Using this function, we can calculate the new states and their probabilities
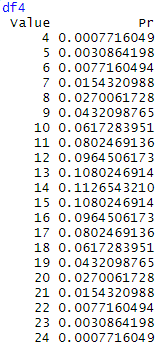
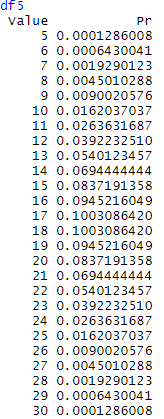
Plotting the probability distribution for the different numbers of dices, is easy to observe that when more dices are added, the global probability peaks to a concrete value.
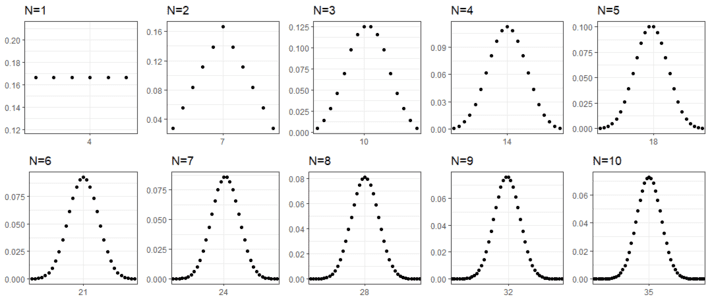
Indistinguishability has introduced symmetry and symmetry has modified the probability distribution making some states more likely than others.
This of course brings a significant reduction in the uncertainty and consequently in the entropy.
To calculate the entropy of the system using indistinguishable states we use this function
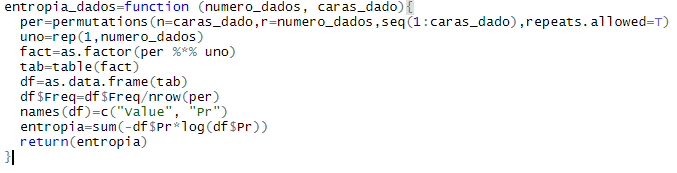
Plotting the entropy per dice for every n, we can see that it decreases with n.
The value for n=1 is 1.792, that is the unitary value for entropy, when n increases, the symmetry starts to reduce the value.
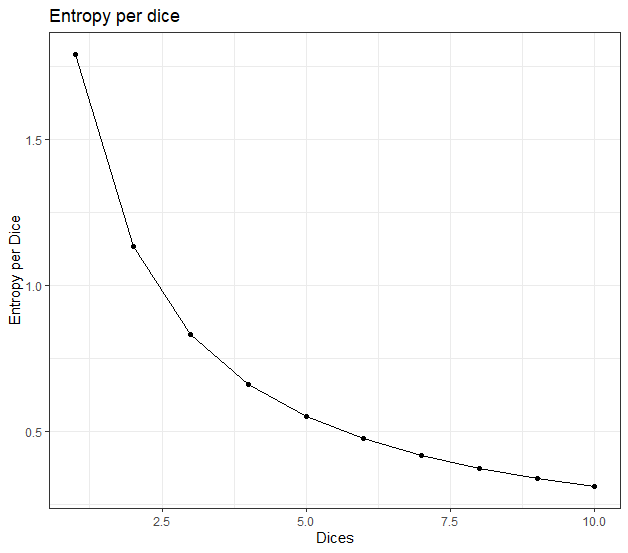
In a system without Indistinguishability the entropy would be 1.792·n for every n.
