
Nowadays, artificial intelligence is present in almost every part of our lives. Smartphones, social media feeds, recommendation engines, online ad networks, and navigation tools are examples of AI-based applications that affect us on a daily basis.
Deep learning has been systematically improving the state of the art in areas such as speech recognition, autonomous driving, machine translation, and visual object recognition. However, the reasons why deep learning works so spectacularly well are not yet fully understood.
Hints from Mathematics
Paul Dirac, one of the fathers of quantum mechanics and arguably the greatest English physicist since Sir Isaac Newton, once remarked that progress in physics using the “method of mathematical reason” would
“…enable[s] one to infer results about experiments that have not been performed. There is no logical reason why the […] method should be possible at all, but one has found in practice that it does work and meets with reasonable success. This must be ascribed to some mathematical quality in Nature, a quality which the casual observer of Nature would not suspect, but which nevertheless plays an important role in Nature’s scheme.”
— Paul Dirac, 1939
Portrait of Paul Dirac is at the peak of his powers (Wikimedia Commons).
There are many examples in history where purely abstract mathematical concepts eventually led to powerful applications way beyond the context in which they were developed. This article is about one of those examples.
Though I’ve been working with machine learning for a few years now, I’m a theoretical physicist by training, and I have a soft spot for pure mathematics. Lately, I have been particularly interested in the connections between deep learning, pure mathematics, and physics.
This article provides examples of powerful techniques from a branch of mathematics called mathematical analysis. My goal is to use rigorous mathematical results to try to “justify”, at least in some respects, why deep learning methods work so surprisingly well.

Abstract representation of a neural network (source).
A Beautiful Theorem
In this section, I will argue that one of the reasons why artificial neural networks are so powerful is intimately related to the mathematical form of the output of its neurons.
A manuscript by Albert Einstein (source).
I will justify this bold claim using a celebrated theorem originally proved by two Russian mathematicians in the late 50s, the so-called Kolmogorov-Arnold representation theorem.

The mathematicians Andrei Kolmogorov (left) and Vladimir Arnold (right).
Hilbert’s 13th problem
In 1900, David Hilbert, one of the most influential mathematicians of the 20th century, presented a famous collection of problems that effectively set the course of the 20th-century mathematics research.
The Kolmogorov–Arnold representation theorem is related to one of the celebrated Hilbert problems, all of which hugely influenced 20th-century mathematics.
Closing in on the connection with neural networks
A generalization of one of these problems, the 13th problem specifically, considers the possibility that a function of n variables can be expressed as a combination of sums and compositions of just two functions of a single variable which are denoted by Φ and ϕ.
More concretely:
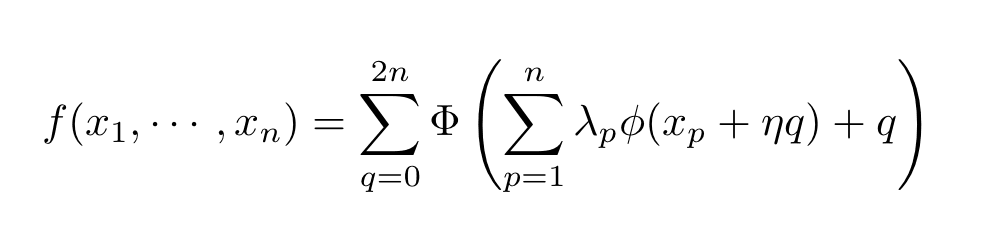
Kolmogorov-Arnold representation theorem
Here, η and the λs are real numbers. It should be noted that these two univariate functions are Φ and ϕ can have a highly complicated (fractal) structure.
Three articles, by Kolmogorov (1957), Arnold (1958) and Sprecher (1965) provided a proof that there must exist such representation. This result is rather unexpected since according to it, the bewildering complexity of multivariate functions can be “translated” into trivial operations of univariate functions, such as additions and function compositions.
Now what?
If you got this far (and I would be thrilled if you did), you are probably wondering: how could an esoteric theorem from the 50s and 60s be even remotely related to cutting-edge algorithms such as artificial neural networks?
A Quick Reminder of Neural Networks Activations
The expressions computed at each node of a neural network are compositions of other functions, in this case, the so-called activation functions. The degree of complexity of such compositions depends on the depth of the hidden layer containing the node. For example, a node in the second hidden layer performs the following computation:
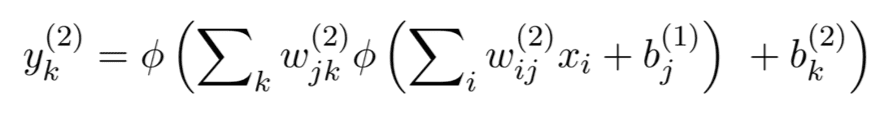
Computation performed by the k-th hidden unit in the second hidden layer.
Where the ws are the weights, and the bs are the biases. The similarity with the multivariate function f shown a few paragraphs above is evident!
Let us quickly write down a function in Python only for forward-propagation which outputs the calculations performed by the neurons. The code for the function below has the following steps:
- First line: the first activation function ϕ acts on the first linear step given by:
x0.dot(w1) + b1
where x0 is the input vector.
- Second line: the second activation function acts on the second linear step
y1.dot(w2) + b2
- Third line: a softmax function is used in the final layer of the neural network, acting on the third linear step
y2.dot(w3) + b3
The full function is:
def forward_propagation(w1, b1, w2, b2, w3, b3, x0):
y1 = phi(x0.dot(w1) + b1)
y2 = phi(y1.dot(w2) + b2)
y3 = softmax(y2.dot(w3) + b3)
return y1, y2, y3
To compare this with our expression above we write:
y2 = phi(phi(x0.dot(w1) + b1).dot(w2) + b2)
The correspondence can be made more clear:
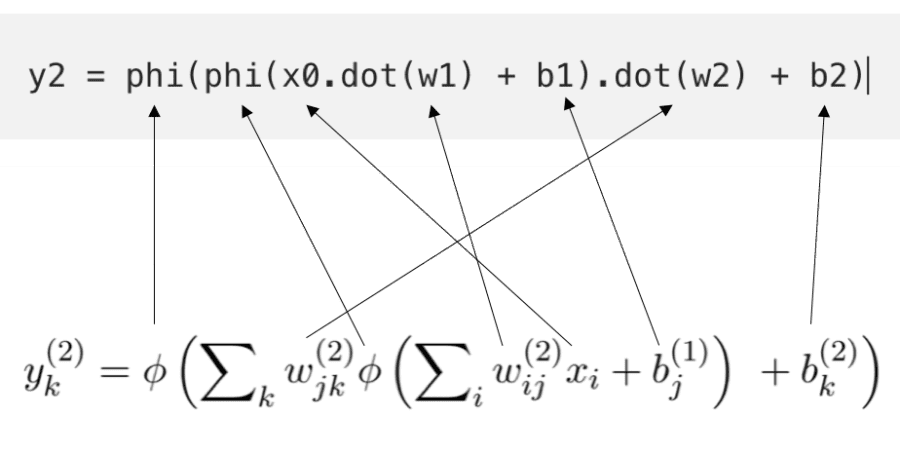
A Connection Between Two Worlds
We, therefore, conclude that the result proved by Kolmogorov, Arnold, and Sprecher implies that neural networks, whose output is nothing but the repeated composition of functions, are extremely powerful objects, which can represent any multivariate function or equivalently almost any process in nature. This partly explains why neural networks work so well in so many fields. In other words, the generalization power of neural networks is, at least in part, a consequence of the Kolmogorov-Arnold representation theorem.
As pointed out by Giuseppe Carleo, the generalization power of forming functions of functions of functions ad nauseam was, in a way, “discovered independently also by nature” since neural networks, which work as shown above doing precisely that, are a simplified way to describe how our brains work.
Thanks a lot for reading! Constructive criticism and feedback are always welcome!
There is a lot more to come, stay tuned!
Originally posted here.
