Bayesian Machine Learning (part – 4)
Introduction
In the previous post we have learnt about the importance of Latent Variables in Bayesian modelling. Now starting from this post, we will see Bayesian in action. We will walk through different aspects of machine learning and see how Bayesian methods will help us in designing the solutions. And also the additional capabilities and insights we can have by using it. The sections which follows are generally known as Bayesian inference. In this post we will see how Bayesian methods can be used to do clustering on the given data.
Probabilistic Clustering
Clustering is the method of splitting the data into separate chunks based on the inherent properties of the data. When we use the word ‘probabilistic’ in it, we imply that each and every point in the given data is a part of every cluster, but with some probability. And thus the word Probabilistic clustering. So let’s start!!!
As it is clear from the heading, each and every point in the given data will belong to every cluster with some probability, and the maximum probability cluster will define the point. Now for such a kind of solution in clustering we need to know few things in advance.
- How each cluster will be defined probabilistically?
- How many clusters will be formed?
Answer to these above 2 questions will help us define each point in the data as a probabilistic part of each cluster. So let us first formulate the solutions to these questions.
How each cluster will be defined probabilistically?
We define each cluster to have come from a Gaussian distribution, having mean = µ and standard deviation = ∑, and the equation looks like
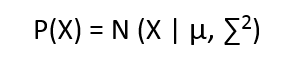
How many clusters will be formed?
To answer this question let us take a sample data set visual :
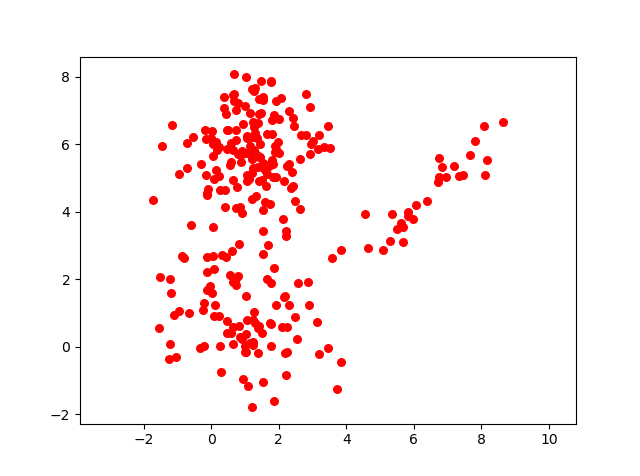
Have a close look to the image above, and you will feel that there are 3 clusters in it. So lets define our 3 clusters probabilistically.
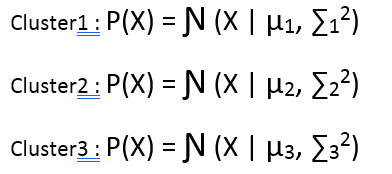
Now, let us try to write an equation which can define the probability of a point in the data to be a part of every cluster, but before that we need a mechanism or a probability function that can tell to which cluster a point can be from with what probability. Suppose for now let us say that a point can be a part of any cluster with equal probability of 1/3. Then the probabilistic distribution of a point would look like:
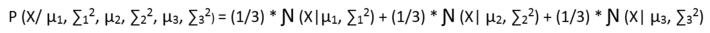
But in the above case it is an assumption that every point can belong from any cluster with equal probability. But is not true right!!So somebody has to tell this, and for it we use a Latent Variable which knows the distribution of every point belonging to every cluster. And the Bayesian model looks like: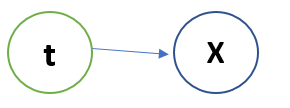
The above model states that Latent Variable t knows, to which cluster the point x belongs and with what probability. So if we re-write the above equation:
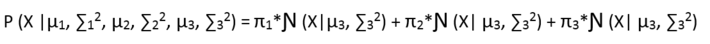
Now let us call all our parameters as
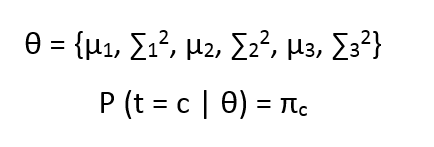
the above equation states that the probability by which the Latent variable takes value c, given all the parameters is πc
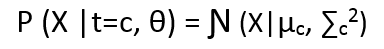
The above equation states that probability of a point sampled from cluster c, given that it has come from cluster c is Ɲ (X|µc, ∑c2).
Now we know that P(X, t=c | θ) = P(X| t=c, θ) * P(t=c | θ) from our Bayesian model. We can marginalize t to compute
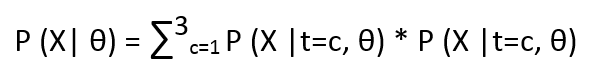
The above equation is exactly same as our original one.
Fact Checks:
- In the equation P (t = c | θ) = πc, this has no condition over the data points x, and thus it can be considered as Prior distribution and as a hard classifier.
- Marginalization was done on t, to have the exact expression on LHS as was chosen originally. Therefore, t remains latent and unobserved.
- Iif we want the probability of a point belonging to a specific cluster, given the parameters θ and the point x, then the expression looks like:
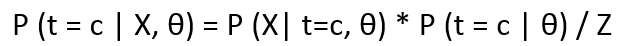
Where LHS is the posterior distribution of t w.r.t X and θ. Z is the normalization constant and can be calculated as :
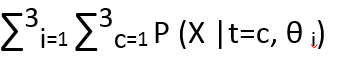
The Chicken-Egg Problem in Probabilistic Clustering
Now it is obvious that the Bayesian model we made between t and x, when we say the latent variable knows the cluster number of every point, we say it probabilistically. That means the formulae applied is the posterior distribution as we discussed in Fact – check section. Now the problem is, to compute θ, we should know t and to compute t, we should know θ. We will see this in the following equations:
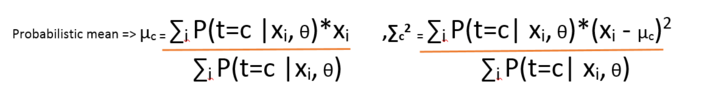
And the posterior t is computed using
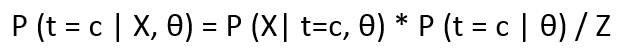
Now, from the above expression it is clear that means and standard deviations are computed if we know the source t and vice-versa.
So, in the next post we will see how to solve the above problem using Expectation – Maximization algorithm.
Thanks for reading!!!
