Gradient Descent has a problem of getting stuck in Local Minima. The following alternatives are available. The following is a summary of answers suggested on CrossValided, originally posted here.
Source for picture: here
First answer
There are many optimization algorithms that operate on a fixed number of real values that are correlated (non-separable). We can divide them roughly in 2 categories: gradient-based optimizers and derivative-free optimizers. Usually you want to use the gradient to optimize neural networks in a supervised setting because that is significantly faster than derivative-free optimization. There are numerous gradient-based optimization algorithms that have been used to optimize neural networks:
- Stochastic Gradient Descent (SGD), minibatch SGD, …: You don’t have to evaluate the gradient for the whole training set but only for one sample or a minibatch of samples, this is usually much faster than batch gradient descent. Minibatches have been used to smooth the gradient and parallelize the forward and backpropagation. The advantage over many other algorithms is that each iteration is in O(n) (n is the number of weights in your NN). SGD usually does not get stuck in local minima (!) because it is stochastic.
- Nonlinear Conjugate Gradient: seems to be very successful in regression, O(n), requires the batch gradient (hence, might not be the best choice for huge datasets)
- L-BFGS: seems to be very successful in classification, uses Hessian approximation, requires the batch gradient
- Levenberg-Marquardt Algorithm (LMA): This is actually the best optimization algorithm that I know. It has the disadvantage that its complexity is roughly O(n^3). Don’t use it for large networks!
And there have been many other algorithms proposed for optimization of neural networks, you could google for Hessian-free optimization or v-SGD (there are many types of SGD with adaptive learning rates, see e.g. here).
Optimization for NNs is not a solved problem! In my experiences the biggest challenge is not to find a good local minimum. However, the challenges are to get out of very flat regions, deal with ill-conditioned error functions etc. That is the reason why LMA and other algorithms that use approximations of the Hessian usually work so well in practice and people try to develop stochastic versions that use second order information with low complexity. However, often a very well tuned parameter set for minibatch SGD is better than any complex optimization algorithm.
Usually you don’t want to find a global optimum. Because that usually requires overfitting the training data.
Second answer
I know this thread is quite old and others have done a great job to explain concepts like local minima, overfitting etc. However, as OP was looking for an alternative solution, I will try to contribute one and hope it will inspire more interesting ideas.
The idea is to replace every weight w to w + t, where t is a random number following Gaussian distribution. The final output of the network is then the average output over all possible values of t. This can be done analytically. You can then optimize the problem either with gradient descent or LMA or other optimization methods. Once the optimization is done, you have two options. One option is to reduce the sigma in the Gaussian distribution and do the optimization again and again until sigma reaches to 0, then you will have a better local minimum (but potentially it could cause overfitting). Another option is keep using the one with the random number in its weights, it usually has better generalization property.
The first approach is an optimization trick (I call it as convolutional tunneling, as it use convolution over the parameters to change the target function), it smooth out the surface of the cost function landscape and get rid of some of the local minima, thus make it easier to find global minimum (or better local minimum).
The second approach is related to noise injection (on weights). Notice that this is done analytically, meaning that the final result is one single network, instead of multiple networks.
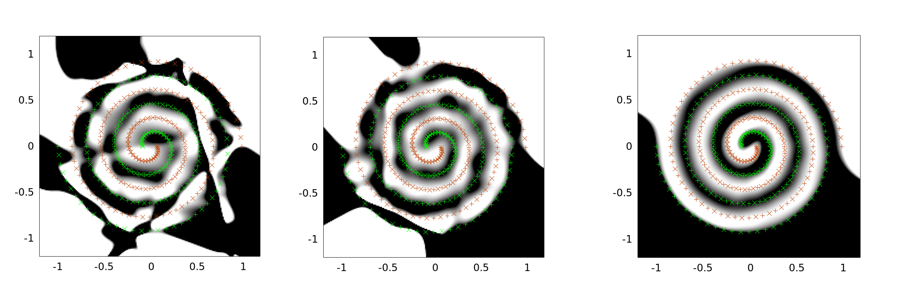
The followings are example outputs for two-spirals problem. The network architecture is the same for all three of them: there is only one hidden layer of 30 nodes, and the output layer is linear. The optimization algorithm used is LMA. The left image is for vanilla setting; the middle is using the first approach (namely repeatedly reducing sigma towards 0); the third is using sigma = 2.
You can see that the vanilla solution is the worst, the convolutional tunneling does a better job, and the noise injection (with convolutional tunneling) is the best (in terms of generalization property).
Both convolutional tunneling and the analytical way of noise injection are my original ideas. Maybe they are the alternative someone might be interested. The details can be found in my paper Combining Infinity Number Of Neural Networks Into One. Warning: I am not a professional academic writer and the paper is not peer reviewed. If you have questions about the approaches I mentioned, please leave a comment.
Third answer
When it comes to Global Optimisation tasks (i.e. attempting to find a global minimum of an objective function) you might wanna take a look at:
- Pattern Search (also known as direct search, derivative-free search, or black-box search), which uses a pattern to determine the points to search at next iteration.
- Genetic Algorithm that uses the concept of mutation, crossover and selection to define the population of points to be evaluated at next iteration of the optimisation.
- Particle Swarm Optimisation that defines a set of particles that “walk” through the space searching for the minimum.
- Surrogate Optimisation that uses a surrogate model to approximate the objective function. This method can be used when the objective function is expensive to evaluate.
- Multi-objective Optimisation (also known as Pareto optimisation) which can be used for the problem that cannot be expressed in a form that has a single objective function (but rather a vector of objectives).
- Simulated Annealing, which uses the concept of annealing (or temperature) to trade-off exploration and exploitation. It proposes new points for evaluation at each iteration, but as the number of iteration increases, the “temperature” drops and the algorithm becomes less and less likely to explore the space thus “converging” towards its current best candidate.
As mentioned above, Simulated Annealing, Particle Swarm Optimisation and Genetic Algorithms are good global optimisation algorithms that navigate well through huge search spaces and unlike Gradient Descent do not need any information about the gradient and could be successfully used with black-box objective functions and problems that require running simulations.