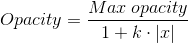Update Sep. 2016: A model with less than a third of the error can be found here.
KIC 8462852 is a star that has been getting a fair amount of attention. It occasionally has unusual dips in brightness, according to Kepler telescope observations. Natural explanations for the dips have been unsatisfactory so far. The hypothesis that we might be looking at transits of alien megastructures has therefore not been ruled out.
Coming up with models of possible transiting objects is a challenging Data Science problem. I have been running simulations and trying to optimize models that replicate simulated transits.
For any transit, it’s usually possible to come up with models that closely match the original light curve, but the shapes of the resulting objects will not necessarily resemble those of the simulation. In machine learning lingo, the error function has numerous and diverse local minima that fit the data almost as well as the global minimum, and it’s difficult for an optimizer to avoid getting stuck in local minima. One way to address this issue is to do hypothesis testing by optimizing for certain assumptions, such as the constraint that the transiting object is spherical or some other shape.
The KIC 8462852 light curves do not look like what you’d expect from a few large and opaque transiting objects. In particular, let’s take a look at the transit that peaks on day 792 (figure below). It’s not just that the light curve is slightly asymmetric and not U-shaped, but let’s also consider how long it lasts. A transit should typically not last 8 days. Jupiter, for example, can traverse the entire diameter of the sun in about a day, and that’s a fairly slow transit.
From simulations of families of objects big and small I can also say that such configurations would not produce a light curve that is so smooth. More generally, I do not believe it’s possible to precisely match the day-792 light curve with a small number of entirely opaque objects.
What is likely required is a swarm or semi-transparent cloud. Let’s take a look at a model based on the hypothesis that opacity of the swarm/gas varies only in the direction of rotation around the star. The optimized model produces the light curve (in red) that you see in the figure above. The fit is quite good (RMSE 0.0036). I also created a short video depicting the modeled transit starting on day 792 and ending just after the start of day 793. The interesting part starts about 10 seconds in.
If you have trouble seeing it, try dragging the video slider back and forth from 00:10 to 00:20.
It’s subtle, but the optimizer seems to have produced — under the constraint I outlined — something that resembles a faint Niven ring. The smooth distribution of the swarm/gas around the structure seems a little hard to explain as the product of an alien civilization, but I suspect it would be harder to come up with a natural explanation for it.
I should emphasize this is not the only possible model. Under different constraints you would get different shapes. This “Niven ring” does produce an excellent fit, nonetheless. Additionally, the debris opacity distribution should be about the same for any model that fits the light curve well. That’s due to the highly unusual features of the day-792 light curve.
Keep in mind we’re modeling opacity, not density. If the debris obstructing the star’s light sits roughly on the surface of an imaginary Dyson sphere, then the response of the model could be interpreted as density. Otherwise, density and opacity are very different things. The following chart shows how opacity varies in the swarm as it’s traversed from left to right.
I used a neural network with custom activation functions to try to get a good fit for the light curve, but the opacity can be roughly approximated with a simple formula:
This is a reasonable model for the decay of density of a gas. It seems pretty obvious it would not be a good model for the decay of opacity of a roughly spherical gaseous object. But it’s not far fetched if we’re talking about a Dyson swarm.
To recap, observations are consistent with a Dyson swarm made up of small objects that distribute in such a way as to form Niven ring-like structures. A model that tests this hypothesis fits the data really well. In contrast, the data taken as a whole does not seem to be nearly as consistent with natural explanations.